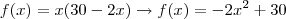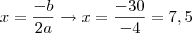por leha » Sáb Jun 13, 2009 19:43
por leha » Sáb Jun 13, 2009 19:43
Pessoal gostaria de pedir a ajuda de voçes para analizar se está certo ou não? Obrigado e fiquem com Deus
De uma longa folha retangular de metal, com 30cm de largura, deve-se fazer uma calha, dobrando as bordas perpendicularmente a folha. quantos centimetros devem se dobrados, de cada lado, de modo que a calha venha a ter capacidade maxima. Gostaria de saber se esta minha resolução está certa caso contrario peço ajuda.
Resolução: f(x)= x(30-2x)
f(x)= -2x²+30x
f'(x)=-4x+30
f''(x)= x=30/4=7,5
Teste para x=7,5 na derivada de 2°ordem f''(x)
f''(7.5)= 7,5<0
fmaximo= f(7,5)= 2(7,5)^2 + 30(7,5)
= 30+225=255
fmaximo=255
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por leha » Ter Jun 16, 2009 00:55
por leha » Ter Jun 16, 2009 00:55
E ai pessoal será que ninguem pode me ajudar a analizar essa questão para ver se esta certa?
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por Molina » Ter Jun 16, 2009 01:03
por Molina » Ter Jun 16, 2009 01:03
Oi leah,
Desculpe, mas da onde você tirou esta função: f(x)= x(30-2x) ?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por leha » Ter Jun 16, 2009 09:09
por leha » Ter Jun 16, 2009 09:09
Meu amigo molina essa função saiu do problema postado abaixo. O negocio é tentar montar a função e derivar e ai aplicar para ver se ela é maximo e minimo. Por isso eu não sei se está função esta certa. Podes me ajudar. Abraço e fique com Deus
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por leha » Ter Jun 16, 2009 09:10
por leha » Ter Jun 16, 2009 09:10
Meu amigo molina essa função saiu do problema postado abaixo. O negocio é tentar montar a função e derivar e ai aplicar para ver se ela é maximo e minimo. Por isso eu não sei se está função esta certa. Podes me ajudar. Abraço e fique com Deus
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por Marcampucio » Ter Jun 16, 2009 13:32
por Marcampucio » Ter Jun 16, 2009 13:32
A solução que você deu está correta
leha. Só para confirmar, note que a função da secção da calha é uma parábola com a concavidade para baixo, cujo vértice é o seu ponto de máximo.
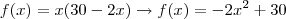
o vértice está em
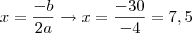
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2263 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7481 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4957 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2969 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1997 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.