 por ARCS » Sex Fev 10, 2012 19:12
por ARCS » Sex Fev 10, 2012 19:12
Estou estudando as demonstrações dos métodos de integração numérica, um destes métodos é a Regra do Trapézio (RT). A demostração da RT pode ser feita usando o polinômio de Newton ou de Lagrange (os mesmos usados para interpolação). O problema é que eu não entendi a seguinte passagem ( o cálculo de um simples integral) :
![\int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{(x-a)^2}{2}\right]_{a}^{b} \int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{(x-a)^2}{2}\right]_{a}^{b}](/latexrender/pictures/b80f2452f2b556ef7ef17cf4c9d32cb9.png)
(1)
isso não seria
![\int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{x^2}{2}-ax\right]_{a}^{b} \int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{x^2}{2}-ax\right]_{a}^{b}](/latexrender/pictures/397a3f7df0e51916fbb6f471852b7e8a.png)
(2)
Usando (1) chega-se a fórmula correta.
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Sáb Fev 11, 2012 11:34
por LuizAquino » Sáb Fev 11, 2012 11:34
ARCS escreveu:![\int_{a}^{b} f[a,b] (x-a) \, dx = f[a,b] \left[ \frac{(x-a)^2}{2}\right]_{a}^{b} \int_{a}^{b} f[a,b] (x-a) \, dx = f[a,b] \left[ \frac{(x-a)^2}{2}\right]_{a}^{b}](/latexrender/pictures/e330afc042619b15c6a40f5db4ce5575.png)
(1)
isso não seria
![\int_{a}^{b} f[a,b] (x-a) \, dx = f[a,b] \left[ \frac{x^2}{2}-ax\right]_{a}^{b} \int_{a}^{b} f[a,b] (x-a) \, dx = f[a,b] \left[ \frac{x^2}{2}-ax\right]_{a}^{b}](/latexrender/pictures/cd9474e3e13e6b5f979d3375af654afc.png)
(2)
Tanto faz.
Usando a substituição u = x - a e du = dx, temos que:
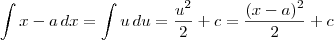
Podemos ainda resolver a integral de outra forma:
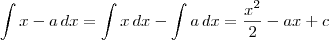
Ambas as primitivas são corretas. Além disso, note que:
![\int_a^b x -a \, dx = \left[\frac{(x-a)^2}{2}\right]_a^b = \frac{(b-a)^2}{2} \int_a^b x -a \, dx = \left[\frac{(x-a)^2}{2}\right]_a^b = \frac{(b-a)^2}{2}](/latexrender/pictures/a6e866b3d2850ce7c6118ab9a7e20225.png)
![\int_a^b x - a \, dx = \left[\frac{x^2}{2} - ax\right]_a^b = \frac{b^2}{2} - ab - \frac{a^2}{2} + a^2 = \frac{b^2 -2ab + a^2}{2} = \frac{(b-a)^2}{2} \int_a^b x - a \, dx = \left[\frac{x^2}{2} - ax\right]_a^b = \frac{b^2}{2} - ab - \frac{a^2}{2} + a^2 = \frac{b^2 -2ab + a^2}{2} = \frac{(b-a)^2}{2}](/latexrender/pictures/2df6b949d8b2920bcd88c7d2a26aa64c.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demostração
por Balanar » Dom Ago 29, 2010 05:43
- 1 Respostas
- 951 Exibições
- Última mensagem por Douglasm

Dom Ago 29, 2010 15:56
Álgebra Elementar
-
- Demostração das identidades trigonometricas
por Alerecife » Sáb Set 08, 2012 13:32
- 3 Respostas
- 1940 Exibições
- Última mensagem por MarceloFantini

Dom Set 09, 2012 17:45
Trigonometria
-
- Sistemas Lineares e demostração de LI e LD?
por Alerecife » Sáb Abr 27, 2013 22:57
- 1 Respostas
- 7039 Exibições
- Última mensagem por Alerecife

Ter Abr 30, 2013 23:16
Álgebra
-
- Problema enolvendo conjuntos, demostração e provas
por moyses » Ter Mai 01, 2012 20:50
- 4 Respostas
- 2215 Exibições
- Última mensagem por moyses

Qua Mai 02, 2012 10:08
Conjuntos
-
- [Limite de Funções de duas variáveis] Demostração
por ARCS » Dom Out 21, 2012 20:15
- 1 Respostas
- 2163 Exibições
- Última mensagem por MarceloFantini

Dom Out 21, 2012 22:04
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{(x-a)^2}{2}\right]_{a}^{b} \int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{(x-a)^2}{2}\right]_{a}^{b}](/latexrender/pictures/b80f2452f2b556ef7ef17cf4c9d32cb9.png) (1)
(1)![\int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{x^2}{2}-ax\right]_{a}^{b} \int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{x^2}{2}-ax\right]_{a}^{b}](/latexrender/pictures/397a3f7df0e51916fbb6f471852b7e8a.png) (2)
(2)
![\int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{(x-a)^2}{2}\right]_{a}^{b} \int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{(x-a)^2}{2}\right]_{a}^{b}](/latexrender/pictures/b80f2452f2b556ef7ef17cf4c9d32cb9.png) (1)
(1)![\int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{x^2}{2}-ax\right]_{a}^{b} \int_{a}^{b} f[a,b] (x-a) dx = f[a,b] \left[ \frac{x^2}{2}-ax\right]_{a}^{b}](/latexrender/pictures/397a3f7df0e51916fbb6f471852b7e8a.png) (2)
(2)
(1)
(2)
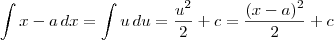
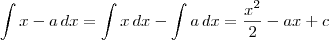
![\int_a^b x -a \, dx = \left[\frac{(x-a)^2}{2}\right]_a^b = \frac{(b-a)^2}{2} \int_a^b x -a \, dx = \left[\frac{(x-a)^2}{2}\right]_a^b = \frac{(b-a)^2}{2}](/latexrender/pictures/a6e866b3d2850ce7c6118ab9a7e20225.png)
![\int_a^b x - a \, dx = \left[\frac{x^2}{2} - ax\right]_a^b = \frac{b^2}{2} - ab - \frac{a^2}{2} + a^2 = \frac{b^2 -2ab + a^2}{2} = \frac{(b-a)^2}{2} \int_a^b x - a \, dx = \left[\frac{x^2}{2} - ax\right]_a^b = \frac{b^2}{2} - ab - \frac{a^2}{2} + a^2 = \frac{b^2 -2ab + a^2}{2} = \frac{(b-a)^2}{2}](/latexrender/pictures/2df6b949d8b2920bcd88c7d2a26aa64c.png)






