 por Scheu » Sex Fev 03, 2012 00:32
por Scheu » Sex Fev 03, 2012 00:32
Desculpem postar uma nova pegunta, mas é que essas questões estão tirando meu sono. Nos exercícios que estou estudando tem a seguinte questão: Demostre que
![\lim_{x\rightarrow a}\left[f(x)+g(x) \right] \lim_{x\rightarrow a}\left[f(x)+g(x) \right]](/latexrender/pictures/ace819773fa4fcc9d3ff983e0f519e3b.png)
pode existir, mesmo que
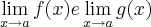
não existam. Minha duvida esta se essa preposição é realmente verdadeira? Por quê? Mais uma vez obrigada.
-
Scheu
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Fev 01, 2012 23:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: cursando
 por LuizAquino » Sex Fev 03, 2012 00:58
por LuizAquino » Sex Fev 03, 2012 00:58
Scheu escreveu:Nos exercícios que estou estudando tem a seguinte questão: Demostre que
![\lim_{x\rightarrow a}\left[f(x)+g(x) \right] \lim_{x\rightarrow a}\left[f(x)+g(x) \right]](/latexrender/pictures/ace819773fa4fcc9d3ff983e0f519e3b.png)
pode existir, mesmo que
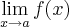
e

não existam. Minha duvida esta se essa preposição é realmente verdadeira? Por quê?
Em alguns casos a resposta é sim: o limite dessa soma pode existir mesmo que o limite de cada parcela não exista.
ExemploConsidere as funções:


Note que

e
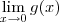
não existem (já que os seus limites laterais são distintos).
Por outro lado, temos que:
![\lim_{x\to 0} [f(x) + g(x)] = \lim_{x\to 0} 2 = 2 \lim_{x\to 0} [f(x) + g(x)] = \lim_{x\to 0} 2 = 2](/latexrender/pictures/05e968382fb7afadc2046cb4b335f939.png)
Portanto, obtemos que
![\lim_{x\to 0} [f(x) + g(x)] \lim_{x\to 0} [f(x) + g(x)]](/latexrender/pictures/95339e5689f458c8e6cfd0f804a3cfc4.png)
existe.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] - Questões teoricas
por Scheu » Sex Fev 03, 2012 00:16
- 1 Respostas
- 1351 Exibições
- Última mensagem por LuizAquino

Sex Fev 03, 2012 00:38
Cálculo: Limites, Derivadas e Integrais
-
- Questões de Limites
 por Luciana » Qua Jun 02, 2010 02:05
por Luciana » Qua Jun 02, 2010 02:05
- 1 Respostas
- 2773 Exibições
- Última mensagem por genivaldouff

Seg Jun 07, 2010 02:20
Cálculo: Limites, Derivadas e Integrais
-
- [Dúvida] Questões de limites
por Jhonata » Qua Mai 29, 2013 19:02
- 0 Respostas
- 1045 Exibições
- Última mensagem por Jhonata

Qua Mai 29, 2013 19:02
Cálculo: Limites, Derivadas e Integrais
-
- [estatística] distribuições teóricas
por titalaferreira » Qui Jun 19, 2008 14:34
- 1 Respostas
- 3443 Exibições
- Última mensagem por admin

Sex Jun 20, 2008 18:01
Dúvidas Pendentes (aguardando novos colaboradores)
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5413 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow a}\left[f(x)+g(x) \right] \lim_{x\rightarrow a}\left[f(x)+g(x) \right]](/latexrender/pictures/ace819773fa4fcc9d3ff983e0f519e3b.png) pode existir, mesmo que
pode existir, mesmo que 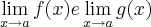 não existam. Minha duvida esta se essa preposição é realmente verdadeira? Por quê? Mais uma vez obrigada.
não existam. Minha duvida esta se essa preposição é realmente verdadeira? Por quê? Mais uma vez obrigada.
![\lim_{x\rightarrow a}\left[f(x)+g(x) \right] \lim_{x\rightarrow a}\left[f(x)+g(x) \right]](/latexrender/pictures/ace819773fa4fcc9d3ff983e0f519e3b.png) pode existir, mesmo que
pode existir, mesmo que 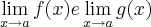 não existam. Minha duvida esta se essa preposição é realmente verdadeira? Por quê? Mais uma vez obrigada.
não existam. Minha duvida esta se essa preposição é realmente verdadeira? Por quê? Mais uma vez obrigada.
pode existir, mesmo que
e
não existam. Minha duvida esta se essa preposição é realmente verdadeira? Por quê?


 e
e 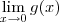 não existem (já que os seus limites laterais são distintos).
não existem (já que os seus limites laterais são distintos).![\lim_{x\to 0} [f(x) + g(x)] = \lim_{x\to 0} 2 = 2 \lim_{x\to 0} [f(x) + g(x)] = \lim_{x\to 0} 2 = 2](/latexrender/pictures/05e968382fb7afadc2046cb4b335f939.png)
![\lim_{x\to 0} [f(x) + g(x)] \lim_{x\to 0} [f(x) + g(x)]](/latexrender/pictures/95339e5689f458c8e6cfd0f804a3cfc4.png) existe.
existe.