 por Scheu » Qui Fev 02, 2012 00:14
por Scheu » Qui Fev 02, 2012 00:14
Ola! atualmente estou estudando o assunto Limites, inicialmente a resolução das primeira questões pareceram fáceis, contudo, tenho grandes dificuldades em resolver questões que ao final aparecem como respostas 0/0 ou k/0. Desta forma, peço ajuda no que tange a resolução de alguns exercícios referentes a esses assuntos:
1-

onde devo achar o

. Tentando resolver cheguei a:

. Chegando nesse ponto o professor falou que constitui uma impossibilidade, mas que da para fazer através de jogo de sinais, entretanto ainda não consegui resolver.
2- Quanto as indeterminações, peço que me ajude exemplificando todos os métodos possíveis para resolve-las.
a)

, onde

, resolvendo achei:


b)
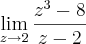
, resolvendo achei:

c)

, resolvendo achei:

.
Desde já agradeço a ajuda
Atenciosamente,
Scheila Borges
-
Scheu
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Fev 01, 2012 23:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: cursando
 por LuizAquino » Qui Fev 02, 2012 02:56
por LuizAquino » Qui Fev 02, 2012 02:56
Scheu escreveu:1-

onde devo achar o

. Tentando resolver cheguei a:

. Chegando nesse ponto o professor falou que constitui uma impossibilidade, mas que da para fazer através de jogo de sinais, entretanto ainda não consegui resolver.
Eu presumo que a função seja

. Além disso, que o limite seja
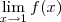
.
Como você já percebeu, quando
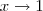
, temos que

. Sendo assim, temos que:

Eu recomendo que você assista a vídeo-aula " 05. Cálculo I - Limites Infinitos" disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquinoScheu escreveu:2- Quanto as indeterminações, peço que me ajude exemplificando todos os métodos possíveis para resolve-las.
a)

, onde

, resolvendo achei:

b)

, resolvendo achei:

c)

, resolvendo achei:

.
a) Qualquer número (exceto o zero) dividido por ele mesmo é igual a 1. Ou seja,

é sempre igual a 1 (exceto quando a = 0). Desse modo, temos que:

b) Usando o produto notável

, temos que:
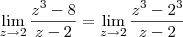



c) Fatorando o polinômio que aparece no denominador, temos que:



 Observação
ObservaçãoPor questão de organização do fórum, nós recomendamos que em cada tópico haja apenas um exercício.
Além disso, vale lembrar que não é objetivo do fórum resolver listas de exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Scheu » Sex Fev 03, 2012 00:03
por Scheu » Sex Fev 03, 2012 00:03
LuizAquino escreveu:Scheu escreveu:1-

onde devo achar o

. Tentando resolver cheguei a:

. Chegando nesse ponto o professor falou que constitui uma impossibilidade, mas que da para fazer através de jogo de sinais, entretanto ainda não consegui resolver.
Eu presumo que a função seja

. Além disso, que o limite seja
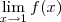
.
Como você já percebeu, quando
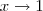
, temos que

. Sendo assim, temos que:

Eu recomendo que você assista a vídeo-aula " 05. Cálculo I - Limites Infinitos" disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquinoScheu escreveu:2- Quanto as indeterminações, peço que me ajude exemplificando todos os métodos possíveis para resolve-las.
a)

, onde

, resolvendo achei:

b)

, resolvendo achei:

c)

, resolvendo achei:

.
a) Qualquer número (exceto o zero) dividido por ele mesmo é igual a 1. Ou seja,

é sempre igual a 1 (exceto quando a = 0). Desse modo, temos que:

b) Usando o produto notável

, temos que:
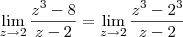



c) Fatorando o polinômio que aparece no denominador, temos que:



 Observação
ObservaçãoPor questão de organização do fórum, nós recomendamos que em cada tópico haja apenas um exercício.
Além disso, vale lembrar que não é objetivo do fórum resolver listas de exercício.
Muito Obrigada pela Ajuda! Valeu
-
Scheu
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Fev 01, 2012 23:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] indeterminação?
por rafaelbr91 » Ter Mar 27, 2012 18:48
- 3 Respostas
- 2231 Exibições
- Última mensagem por nietzsche

Ter Mar 27, 2012 19:31
Cálculo: Limites, Derivadas e Integrais
-
- Indeterminação de Limites
por dsidney30 » Sex Mai 03, 2013 15:53
- 1 Respostas
- 1552 Exibições
- Última mensagem por young_jedi

Dom Mai 05, 2013 19:07
Cálculo: Limites, Derivadas e Integrais
-
- Indeterminação limites fundamental
por Rosi7 » Sex Mai 22, 2015 11:49
- 3 Respostas
- 4751 Exibições
- Última mensagem por Jennicop

Ter Dez 22, 2015 03:20
Cálculo: Limites, Derivadas e Integrais
-
- Limites - Indeterminação do tipo 0X+infinito
por Pollyanna Moraes » Sáb Abr 28, 2012 15:04
- 1 Respostas
- 2956 Exibições
- Última mensagem por Guill

Dom Abr 29, 2012 09:05
Cálculo: Limites, Derivadas e Integrais
-
- [Limites e Continuidade] - Sair da Indeterminação
por Cassiano » Ter Set 25, 2012 11:41
- 2 Respostas
- 2329 Exibições
- Última mensagem por Cassiano

Qua Set 26, 2012 09:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 onde devo achar o
onde devo achar o  . Tentando resolver cheguei a:
. Tentando resolver cheguei a:  . Chegando nesse ponto o professor falou que constitui uma impossibilidade, mas que da para fazer através de jogo de sinais, entretanto ainda não consegui resolver.
. Chegando nesse ponto o professor falou que constitui uma impossibilidade, mas que da para fazer através de jogo de sinais, entretanto ainda não consegui resolver. , onde
, onde  , resolvendo achei:
, resolvendo achei: 

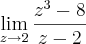 , resolvendo achei:
, resolvendo achei: 
 , resolvendo achei:
, resolvendo achei:  .
.

 . Além disso, que o limite seja
. Além disso, que o limite seja 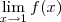 .
.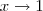 , temos que
, temos que  . Sendo assim, temos que:
. Sendo assim, temos que:
 , resolvendo achei:
, resolvendo achei: 
 , resolvendo achei:
, resolvendo achei: 
 , resolvendo achei:
, resolvendo achei:  é sempre igual a 1 (exceto quando a = 0). Desse modo, temos que:
é sempre igual a 1 (exceto quando a = 0). Desse modo, temos que:
 , temos que:
, temos que: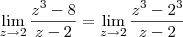










 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.