 por iel » Seg Jun 01, 2009 22:38
por iel » Seg Jun 01, 2009 22:38
?(P+S)/(P[(r-1)P-S]) dp , onde r e s são constantes.
quem po der ajudar, ficarei grato.. (essa eu não conseguir desenrolar)
?tg³xdx tá certo galera? VALEEEEU
? tan³ x dx
? tan² x tan x dx
? (sen² x)/(cos² x) tan x dx
? (sen² x)(tan x) (dx / cos² x)
? (1 - cos² x)(tan x)(dx / cos² x)
? [ 1 - 1/(tan² x + 1) ](tan x)(dx / cos² x)
u = tan x
du = dx / cos² x
? [ 1 - 1/(u² + 1) ] u du
? [ u - u/(u² + 1) ] du
? u du - ? [ u / (u² + 1) ] du
= u²/2 - (1/2) ? [ 2u / (u² + 1) ] du
= u²/2 - (1/2) [ ln?u² + 1? + cte ]
-
iel
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jun 01, 2009 20:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Quimica
- Andamento: cursando
 por Molina » Ter Jun 02, 2009 06:24
por Molina » Ter Jun 02, 2009 06:24
iel escreveu:?tg³xdx tá certo galera? VALEEEEU
? tan³ x dx
? tan² x tan x dx
? (sen² x)/(cos² x) tan x dx
? (sen² x)(tan x) (dx / cos² x)
? (1 - cos² x)(tan x)(dx / cos² x)
? [ 1 - 1/(tan² x + 1) ](tan x)(dx / cos² x)
u = tan x
du = dx / cos² x
? [ 1 - 1/(u² + 1) ] u du
? [ u - u/(u² + 1) ] du
? u du - ? [ u / (u² + 1) ] du
= u²/2 - (1/2) ? [ 2u / (u² + 1) ] du
= u²/2 - (1/2) [ ln?u² + 1? + cte ]
Bom dia.
Acho que seu raciocínio está certo sim.
Você poderia tambem ter utilizado as fórmulas de integrações trigonométricas:
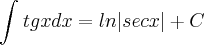
(para n = 1)
e

Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- constantes de proporcionalidades
por Fabricio dalla » Qui Mar 31, 2011 17:47
- 1 Respostas
- 1619 Exibições
- Última mensagem por Elcioschin

Qui Mar 31, 2011 19:09
Álgebra Elementar
-
- valores das constantes a e b
por Douglas16 » Dom Mar 31, 2013 16:36
- 6 Respostas
- 6308 Exibições
- Última mensagem por e8group

Seg Abr 01, 2013 13:31
Cálculo: Limites, Derivadas e Integrais
-
- (Limites) Encontrar as constantes
 por Haahs » Qua Nov 04, 2009 00:32
por Haahs » Qua Nov 04, 2009 00:32
- 7 Respostas
- 6931 Exibições
- Última mensagem por Lucio Carvalho

Dom Abr 20, 2014 20:32
Cálculo
-
- Limites com constantes positivas
por EulaCarrara » Qua Abr 21, 2010 15:59
- 2 Respostas
- 2157 Exibições
- Última mensagem por MarceloFantini

Qua Abr 21, 2010 18:43
Cálculo: Limites, Derivadas e Integrais
-
- [Sistemas de equações] Como se chegar a estas constantes?
por Wilson de Andrade » Dom Mar 11, 2012 16:08
- 2 Respostas
- 1799 Exibições
- Última mensagem por LuizAquino

Seg Mar 12, 2012 01:23
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


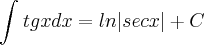 (para n = 1)
(para n = 1)


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
