 por adomingues » Sex Jan 20, 2012 16:45
por adomingues » Sex Jan 20, 2012 16:45
Boa tarde
Estou a tentar resolver este integral, mas não chego ao resultado certo
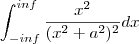
cujo resultado é
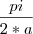
Recorrendo a uma tabela de integrais sei que
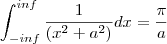
No entanto não estou a conseguir usar a regra para chegar ao resultado correcto
Desde já obrigado
-
adomingues
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Jan 20, 2012 16:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Andamento: cursando
 por ant_dii » Sáb Jan 21, 2012 01:57
por ant_dii » Sáb Jan 21, 2012 01:57
De modo geral pode-se fazer o seguinte

Por parcelas temos que, de (1)
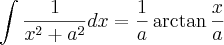
.
E, para (2), faremos
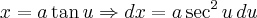
então
![(x^2+a^2)^2=(a^2\tan^2 u+a^2)^2=[a^2(\tan^2 u+1)]^2=a^4\sec^4 u (x^2+a^2)^2=(a^2\tan^2 u+a^2)^2=[a^2(\tan^2 u+1)]^2=a^4\sec^4 u](/latexrender/pictures/ee164dbada922a11bd2c3756fdf0f30a.png)
de onde
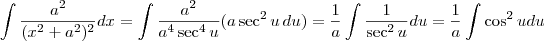
usando
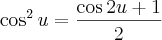
então
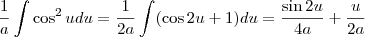
Logo, unindo os resultados para (1) e (2), teremos
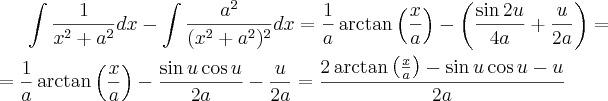
Como
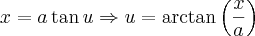
podemos fazer
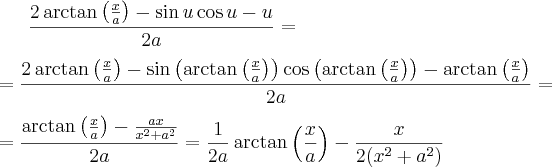
Portanto,
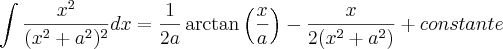
.
Não entendi bem quais eram seus limites de integração, mas agora basta que você os aplique e poderá encontrar a resposta correta...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por ant_dii » Sáb Jan 21, 2012 02:39
por ant_dii » Sáb Jan 21, 2012 02:39
adomingues escreveu:Estou a tentar resolver este integral, mas não chego ao resultado certo
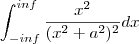
cujo resultado é
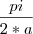
Recorrendo a uma tabela de integrais sei que

Agora entendi os limites de integração. Na verdade você queria
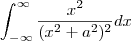
que, de fato, é
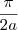
.
Para chegar a esse resultado você terá que usar limites sobre as integrais impróprias. A minha sugestão é que você faça
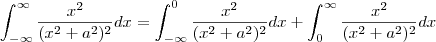
Como no post anterior já coloquei a integral calculada, agora basta que você calcule as integrais sobre os limites de integração e aplique limite para chegar ao resultado...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral - Resolução de integral indefinida.
por brunoisoppo » Qui Mar 03, 2016 15:26
- 0 Respostas
- 3452 Exibições
- Última mensagem por brunoisoppo

Qui Mar 03, 2016 15:26
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de Integral
por suziquim » Qua Jun 08, 2011 13:18
- 4 Respostas
- 2582 Exibições
- Última mensagem por suziquim

Qui Jun 09, 2011 12:04
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de Integral -
por vmouc » Dom Ago 21, 2011 15:01
- 2 Respostas
- 1834 Exibições
- Última mensagem por Neperiano

Dom Ago 21, 2011 15:25
Cálculo: Limites, Derivadas e Integrais
-
- RESOLUÇÃO DE INTEGRAL
por anselmojr97 » Ter Set 22, 2015 11:06
- 2 Respostas
- 2275 Exibições
- Última mensagem por anselmojr97

Ter Set 22, 2015 11:45
Cálculo: Limites, Derivadas e Integrais
-
- resolução derivada integral
por MARCIOESTUDIOSO » Seg Fev 14, 2011 10:33
- 4 Respostas
- 4107 Exibições
- Última mensagem por LuizAquino

Ter Fev 15, 2011 14:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
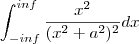 cujo resultado é
cujo resultado é 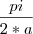


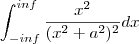 cujo resultado é
cujo resultado é 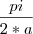



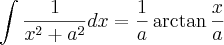 .
.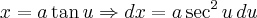
![(x^2+a^2)^2=(a^2\tan^2 u+a^2)^2=[a^2(\tan^2 u+1)]^2=a^4\sec^4 u (x^2+a^2)^2=(a^2\tan^2 u+a^2)^2=[a^2(\tan^2 u+1)]^2=a^4\sec^4 u](/latexrender/pictures/ee164dbada922a11bd2c3756fdf0f30a.png)
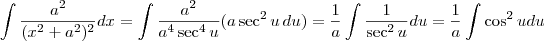
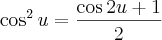
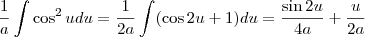
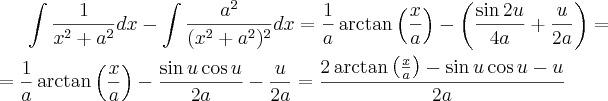
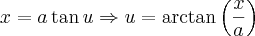

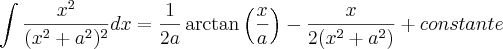 .
.
cujo resultado é

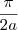 .
.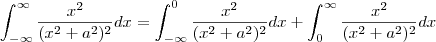

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.