 por Aliocha Karamazov » Sex Nov 25, 2011 00:28
por Aliocha Karamazov » Sex Nov 25, 2011 00:28
Pessoal, estou com problemas nesse limite:
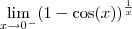
Comecei assim:
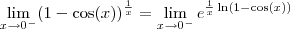
Então, tentei calcular
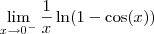

vai para

, mas não entendi o
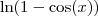
. Isso é a mesma coisa que calcular
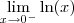
, mas essa função nem existe para x negativo. No entanto, entrei no site wolframalpha e vi isso
http://www.wolframalpha.com/input/?i=li ... +ln%28x%29.
Ou seja,
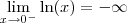
Como pode isso?
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Sex Nov 25, 2011 10:20
por LuizAquino » Sex Nov 25, 2011 10:20
Aliocha Karamazov escreveu:(...)
Então, tentei calcular
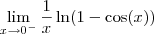

vai para

, mas não entendi o
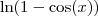
. Isso é a mesma coisa que calcular
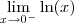
Não é a mesma coisa.
Observe o círculo trigonométrico abaixo.
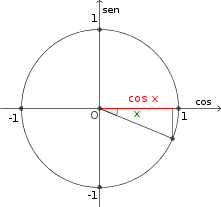
- figura.png (4.83 KiB) Exibido 1947 vezes
Note que para x próximo de 0 pela esquerda (ou seja, x é um ângulo próximo de zero e negativo), temos que
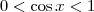
. Isso significa que
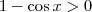
quando
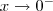
.
Sendo assim, calcular
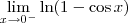
seria equivalente a calcular
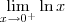
.
A explicação é simples: o programa errou.
Muito provavelmente o programa interpretou
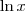
como se fosse
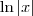
.
ObservaçãoVale lembrar que um ângulo negativo significa que ele foi marcado no sentido horário. Já um ângulo positivo significa que ele foi marcado no sentido anti-horário. Veja um exemplo na figura abaixo.
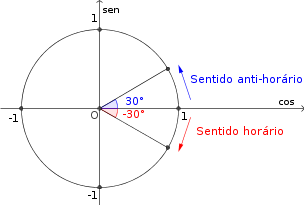
- ângulos.png (6.9 KiB) Exibido 1947 vezes
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Aliocha Karamazov » Sex Nov 25, 2011 21:21
por Aliocha Karamazov » Sex Nov 25, 2011 21:21
Entendi, Luiz. Obrigado.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Indeterminação - Limite
por Paloma » Ter Mar 16, 2010 21:06
- 10 Respostas
- 9735 Exibições
- Última mensagem por Paloma

Sáb Mar 20, 2010 13:57
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminação 0/0
por ravi » Ter Mai 08, 2012 06:42
- 1 Respostas
- 1388 Exibições
- Última mensagem por LuizAquino

Ter Mai 08, 2012 12:13
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida: Limite com indeterminação 0/0
por Samira » Sáb Nov 27, 2010 20:04
- 3 Respostas
- 3348 Exibições
- Última mensagem por andrefahl

Dom Nov 28, 2010 00:06
Cálculo: Limites, Derivadas e Integrais
-
- [Limite no infinito]casos de indeterminação
por moyses » Sex Set 09, 2011 00:24
- 9 Respostas
- 5678 Exibições
- Última mensagem por LuizAquino

Seg Set 12, 2011 12:18
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo de limite] quando há indeterminação 0/0
por JessicaDias » Qui Abr 12, 2012 20:00
- 2 Respostas
- 3001 Exibições
- Última mensagem por JessicaDias

Qui Abr 12, 2012 21:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
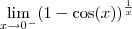
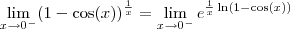
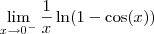
 vai para
vai para  , mas não entendi o
, mas não entendi o 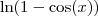 . Isso é a mesma coisa que calcular
. Isso é a mesma coisa que calcular 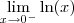 , mas essa função nem existe para x negativo. No entanto, entrei no site wolframalpha e vi isso http://www.wolframalpha.com/input/?i=li ... +ln%28x%29.
, mas essa função nem existe para x negativo. No entanto, entrei no site wolframalpha e vi isso http://www.wolframalpha.com/input/?i=li ... +ln%28x%29.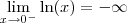


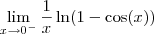
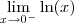
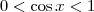 . Isso significa que
. Isso significa que 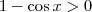 quando
quando 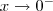 .
.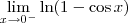 seria equivalente a calcular
seria equivalente a calcular 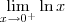 .
.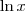 como se fosse
como se fosse 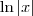 .
.