 por Imscatman » Qui Nov 17, 2011 14:04
por Imscatman » Qui Nov 17, 2011 14:04
Olá!
Tenho duas dúvidas com a prova de
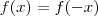
implica

(isto é, que se f é par, então sua derivada f' é ímpar).
Lembrando que:
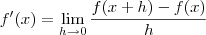
A prova começa assim:

Mas aqui eu já tenho a
primeira dúvida: se em
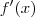
o

é na verdade algo como

, como eu posso fazer

substituindo

por
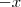
na expressão original, mas sem tocar no

? Parece-me que

passaria a ser

, mas então deixaria de ser

.
Engolindo isso, a prova continua. Terei uma segunda dúvida. Continuando, há esses passos:
![f'(-x)=\lim_{h\rightarrow0}\frac{f[-(x-h)]-f(-x)}{h}=\lim_{h\rightarrow0}\frac{f(x-h)-f(x)}{h} f'(-x)=\lim_{h\rightarrow0}\frac{f[-(x-h)]-f(-x)}{h}=\lim_{h\rightarrow0}\frac{f(x-h)-f(x)}{h}](/latexrender/pictures/8d2c19b80d26726cdf903e23ee4559fb.png)
Aqui ok: como a função é par, os

ficaram
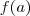
acima. E a seguir introduz-se um sinal de menos dentro e fora do limite. Ok também:

E nesse ponto toma-se

e faz-se:

Isso é

, concluindo a prova. Mas -
segunda dúvida - me incomoda que, no símbolo de limite, a substituição seja

em vez de

. Isso não deveria fazer diferença? Não ficaria

ali?
Agradeço a quem puder me ajudar.
P. S.: tirei essa demonstração do livro (e-book) de respostas do Cálculo vol. 6 (James Stewart).
Atualizado: já posso ver que tanto faz colocar

ou

no limite, porque se um tende a zero, o outro também. Essa é a explicação da segunda dúvida, certo? A primeira dúvida permanece. Pensando aqui...
-

Imscatman
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mar 17, 2011 17:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sex Nov 18, 2011 21:44
por LuizAquino » Sex Nov 18, 2011 21:44
Imscatman escreveu:(...)
A prova começa assim:

Mas aqui eu já tenho a
primeira dúvida: se em f'(x) o h é na verdade algo como

, como eu posso fazer f'(-x) substituindo x por -x na expressão original, mas sem tocar no h? Parece-me que h passaria a ser

, mas então deixaria de ser h.
(...)
Você já sabe que uma forma de definir
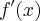
é :

Note que
x representa qualquer valor no domínio de
f. Suponha então que há um número negativo nesse domínio, por exemplo o valor -
a.
A expressão anterior para
x=-
a teria o formato:

Faça então a mudança de variável

(que é o mesmo que

). Note que quando

, temos que

. Sendo assim, podemos reescrever a expressão anterior como:

Agora siga um raciocínio semelhante considerando que o número negativo no domínio seja -
x.
Imscatman escreveu:(...)

E nesse ponto toma-se

e faz-se:

Isso é -f'(x), concluindo a prova. Mas -
segunda dúvida - me incomoda que, no símbolo de limite, a substituição seja

em vez de

. Isso não deveria fazer diferença? Não ficaria

ali?
(...)
Imscatman escreveu:Atualizado: já posso ver que tanto faz colocar

ou

no limite, porque se um tende a zero, o outro também. Essa é a explicação da segunda dúvida, certo?
Ao fazer a substituição

, note que quando

, temos que

. Por isso não há problema algum escrever que:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Problema na "prova" das regras operatórias
por Subject Delta » Qua Abr 25, 2012 17:37
- 2 Respostas
- 2841 Exibições
- Última mensagem por Subject Delta

Qua Abr 25, 2012 21:23
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas - Questão envolvendo prova e angulo
por RuuKaasu » Sáb Dez 26, 2015 23:57
- 0 Respostas
- 1730 Exibições
- Última mensagem por RuuKaasu

Sáb Dez 26, 2015 23:57
Cálculo: Limites, Derivadas e Integrais
-
- Questão envolvendo Derivadas e área! Prova no sábado!!
por arthurvct » Qui Jun 13, 2013 15:21
- 1 Respostas
- 1630 Exibições
- Última mensagem por e8group

Sex Jun 14, 2013 00:49
Cálculo: Limites, Derivadas e Integrais
-
- Problema PRova.
por itroxz » Ter Abr 17, 2012 17:55
- 0 Respostas
- 636 Exibições
- Última mensagem por itroxz

Ter Abr 17, 2012 17:55
Sistemas de Equações
-
- Problema com Derivadas
por carlosvinnicius » Seg Dez 27, 2010 01:08
- 4 Respostas
- 2822 Exibições
- Última mensagem por carlosvinnicius

Seg Dez 27, 2010 14:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
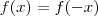 implica
implica  (isto é, que se f é par, então sua derivada f' é ímpar).
(isto é, que se f é par, então sua derivada f' é ímpar).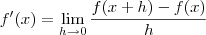

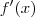 o
o  é na verdade algo como
é na verdade algo como  , como eu posso fazer
, como eu posso fazer  substituindo
substituindo  por
por 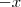 na expressão original, mas sem tocar no
na expressão original, mas sem tocar no  ? Parece-me que
? Parece-me que  passaria a ser
passaria a ser  , mas então deixaria de ser
, mas então deixaria de ser  .
.![f'(-x)=\lim_{h\rightarrow0}\frac{f[-(x-h)]-f(-x)}{h}=\lim_{h\rightarrow0}\frac{f(x-h)-f(x)}{h} f'(-x)=\lim_{h\rightarrow0}\frac{f[-(x-h)]-f(-x)}{h}=\lim_{h\rightarrow0}\frac{f(x-h)-f(x)}{h}](/latexrender/pictures/8d2c19b80d26726cdf903e23ee4559fb.png)
 ficaram
ficaram 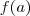 acima. E a seguir introduz-se um sinal de menos dentro e fora do limite. Ok também:
acima. E a seguir introduz-se um sinal de menos dentro e fora do limite. Ok também:
 e faz-se:
e faz-se:
 , concluindo a prova. Mas - segunda dúvida - me incomoda que, no símbolo de limite, a substituição seja
, concluindo a prova. Mas - segunda dúvida - me incomoda que, no símbolo de limite, a substituição seja  em vez de
em vez de  . Isso não deveria fazer diferença? Não ficaria
. Isso não deveria fazer diferença? Não ficaria  ali?
ali? ou
ou  no limite, porque se um tende a zero, o outro também. Essa é a explicação da segunda dúvida, certo? A primeira dúvida permanece. Pensando aqui...
no limite, porque se um tende a zero, o outro também. Essa é a explicação da segunda dúvida, certo? A primeira dúvida permanece. Pensando aqui...


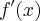 é :
é :

 (que é o mesmo que
(que é o mesmo que  ). Note que quando
). Note que quando  , temos que
, temos que  . Sendo assim, podemos reescrever a expressão anterior como:
. Sendo assim, podemos reescrever a expressão anterior como:
 . Por isso não há problema algum escrever que:
. Por isso não há problema algum escrever que:






