Preciso concluir os 8 passos para esboçar o grafico da funçao: (x^2-1)^3
parei no sexto passo que é determinar a concavidade e os pontos de inflexão, com a derivada 2ª encontrei os seguintes resultados:
x>1 concava para cima e X<-1 concava para baixo. Nao sei se esta certo e o que posso concluir com isso, não tenho ponto de inflexao?



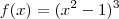 tem dois zeros de multiplicidade 3. São eles -1 e 1.
tem dois zeros de multiplicidade 3. São eles -1 e 1.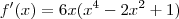 .Quais são os zeros?
.Quais são os zeros?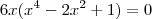
 .
.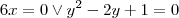
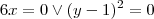
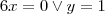
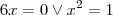

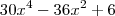 Quais os zeros?
Quais os zeros?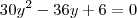
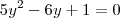
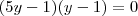
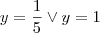
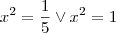
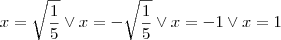

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.