Basicamente: prove pela definição que a função
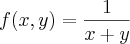é diferenciável.Pra começar que eu assumo que o problema nao esteja falando dos ptos (x,0) e (0,y) mas vamo lá
Pela definição, f só é diferenciável
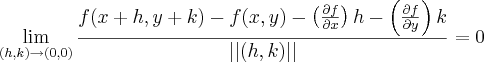
Entao vamos lá. As derivadas parciais são da forma:
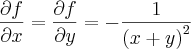correto ? Então o limite fica assim:![\lim_{ (h,k)\rightarrow (0,0 } \left[ \left( \frac{1}{x+h+y+k} - \frac{1}{x+y} + \frac{h}{{(x+y)}^{2}} + \frac{k}{{(x+y)}^{2}} \right)\times \frac{1}{||(h,k)||} \right]](/latexrender/pictures/5340638d89d698ebac7734523e3cece1.png "\lim_{ (h,k)\rightarrow (0,0 } \left[ \left( \frac{1}{x+h+y+k} - \frac{1}{x+y} + \frac{h}{{(x+y)}^{2}} + \frac{k}{{(x+y)}^{2}} \right)\times \frac{1}{||(h,k)||} \right]")
Na minha cabeça isso ja ta meio errado... Se o limite de uma soma é a soma dos limites entao eu ja poderia distribuir o inverso do modulo em todos esses 4 termos e eu ja obteria limites que não existem. tem coisa errada ai né ?
Muito obrigado! Espero ter ficado claro. Por favor, ajudem-me. Obrigado...
.
: