Dois resistores R1 e R2 são conectados em paralelo, e a resistência equivalente R medida em ? é dada por:
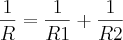
Se R1 e R2 estão variando a uma taxa de 0,1 ?/s e 0,4 ?/s respectivamente,
determinar a taxa de variação de R quando R1=75? e R2=100?
Então:
R1 em função de t (em segundos):
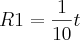
R2 em função de t

Muito bem..
Cheguei na expressão de R em função de t (em segundos):
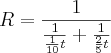
Que é igual a:

Então, a taxa de variação é 2/25, certo?
Mas aonde vai o 75 e o 100??????
Como a função é linear, a derivada não varia, certo? ou seja, o 75 e 100 não servem para nada?
Estou interpretando algo errado, ou o professor colocou esses valores justamente para gerar essa duvida nos alunos?
?
?



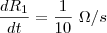
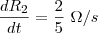
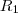 e
e 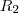 , sendo que eles estão em função do tempo, temos que
, sendo que eles estão em função do tempo, temos que 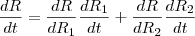
 , que é o mesmo que
, que é o mesmo que  , temos que as derivadas de
, temos que as derivadas de 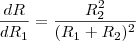

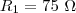 e
e  . Sendo assim, podemos dizer que:
. Sendo assim, podemos dizer que: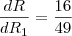



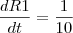
 . Note que há dois coeficientes a determinar:
. Note que há dois coeficientes a determinar:  .
.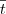 (que não foi fornecido), tal que
(que não foi fornecido), tal que  . Isso não é suficiente para determinar explicitamente o valor de
. Isso não é suficiente para determinar explicitamente o valor de  ,
, 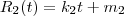 e usando o fato de que
e usando o fato de que 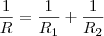 , temos que:
, temos que: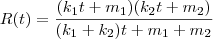

 .
.



