 por teteffs » Qui Out 06, 2011 17:32
por teteffs » Qui Out 06, 2011 17:32
Boa tarde pessoal ,curso Engenharia de Produção e estou com uma dúvida quanto a uma questão de calculo de volume de um solido por integral definida.Estou em duvida quanto ao raio do grafico. A questão é a seguinte: A região R, limitada pela curva y=1/4 x², o eixo x e as retas x=1 e x=4 gira em torno do eixo x. Encontrar o volume do sólido de revolução gerado.
Bom primeiramente eu procurei o xv que é xv=0 ja que em 1/4 x², o xv sendo -b/2a e nao havendo o termo b o resultado é 0. A partir disso em minha tabela de valores de x e y ficaria: Lembrando o xv deu zero entao conto 2 valores antes do zero e 2 valores depois do zero para minha tabela
x y
-2 1 Bom pessoal quando fiz o grafico que resulta em duas parábolas,uma concavidade para cima e a outra para baixo, mas estou em duvida qual sera
-1 1/4 o raio,sei que é algum y,o grafico demonstra isso, mas quando se faz o grafico os valores vao de 0 a 2 ,e ele quer de 1 a 4 portanto creio que o raio
0 0 nao sera somente o y,alguem pode me ajudar a pensar?
1 1/4
2 1
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
 por LuizAquino » Qui Out 06, 2011 18:43
por LuizAquino » Qui Out 06, 2011 18:43
teteffs escreveu:A região R, limitada pela curva y=1/4 x², o eixo x e as retas x=1 e x=4 gira em torno do eixo x. Encontrar o volume do sólido de revolução gerado.
A figura abaixo ilustra a região e o sólido gerado.
Note que cada seção transversal, perpendicular ao eixo x, será um círculo de raio y (sendo que

). Portanto, a área de cada seção será dada por:
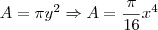
Enxergando a área A como uma função de x, o volume desse sólido será dado por
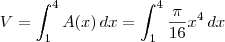
Agora tente terminar o exercício.
ObservaçãoSe deseja revisar esse conteúdo, então eu recomendo a vídeo-aula "38. Cálculo I - Aplicação de Integrais no Cálculo de Volumes". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por teteffs » Sex Out 07, 2011 17:53
por teteffs » Sex Out 07, 2011 17:53
Oi Luiz Aquino mto obrigado pela ajuda entao eu havia pensado como vc e achei este resultado:
CodeCogsEqn.gif
Bom eu nao vejo uma outra maneira de achar o raio a nao ser aquele mas meus colegas de faculdade teimam em dizer q esta errado, que o professor nao concorda!!!
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
 por teteffs » Sex Out 07, 2011 17:56
por teteffs » Sex Out 07, 2011 17:56
teteffs escreveu:Oi Luiz Aquino mto obrigado pela ajuda entao eu havia pensado como vc e achei este resultado:
Bom eu nao vejo uma outra maneira de achar o raio a nao ser aquele mas meus colegas de faculdade teimam em dizer q esta errado, que o professor nao concorda!!!
- Anexos
-
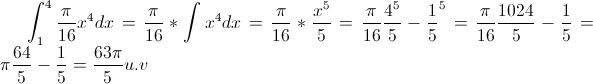
- CodeCogsEqn.gif (2.92 KiB) Exibido 6722 vezes
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
 por LuizAquino » Sex Out 07, 2011 19:11
por LuizAquino » Sex Out 07, 2011 19:11
A solução correta é:
![V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)} V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)}](/latexrender/pictures/69c7666f93f10d57639ba2187096737f.png) Observação
ObservaçãoVeja na figura abaixo que dado um número x no intervalo [1, 4], o valor de y associado a ele (através da curva
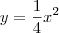
) será o raio do círculo que representa uma seção transversal do sólido.
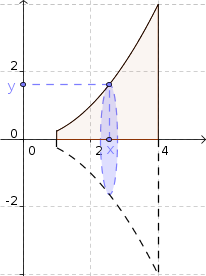
- regiãoR-raio-y.png (81.98 KiB) Exibido 6716 vezes
Editado pela última vez por
LuizAquino em Sex Out 07, 2011 19:28, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por teteffs » Sex Out 07, 2011 19:20
por teteffs » Sex Out 07, 2011 19:20
[quote="LuizAquino"]A solução correta é:
Oiiii então Luis Aquino essa questão é de uma prova que tive,todo mundo da sala errou sabe,muitos fizeram a questao inclusive eu na prova,e o raciocinio era o mesmo que o seu, havia dado este mesmo resultado seu,so que o professor deu a questao que vc resolveu como errada,por isso calculei dessa outra maneira,ele pediu entao q refizessemos essa questao valendo nota,e por isso ainda nao corrigiu a questao,nao entendemos pq p gente dava esse valor seu mesmo mas cmo ele ja deu como errado estamos ficando doidos.
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 19:40
por LuizAquino » Sáb Out 08, 2011 19:40
Se o enunciado do exercício é exatamente como o que você postou, então a resposta correta é como indiquei nas mensagens anteriores.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por teteffs » Sáb Out 08, 2011 20:18
por teteffs » Sáb Out 08, 2011 20:18
LuizAquino escreveu:Se o enunciado do exercício é exatamente como o que você postou, então a resposta correta é como indiquei nas mensagens anteriores.
O enunciado é aquele mesmo,muitissimo obrigado pela ajuda e paciencia, tenha um bom fim de semana,fique com Deus!
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:29
- 1 Respostas
- 1847 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:05
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:48
- 1 Respostas
- 1991 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:07
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:53
- 1 Respostas
- 2025 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 13:29
- 1 Respostas
- 1727 Exibições
- Última mensagem por MarceloFantini

Sex Nov 18, 2011 16:18
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Integral definida..
por Nei Stolberg » Qui Mar 21, 2019 19:11
- 0 Respostas
- 4730 Exibições
- Última mensagem por Nei Stolberg

Qui Mar 21, 2019 19:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ). Portanto, a área de cada seção será dada por:
). Portanto, a área de cada seção será dada por: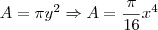
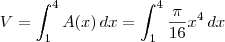

![V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)} V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)}](/latexrender/pictures/69c7666f93f10d57639ba2187096737f.png)
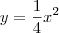 ) será o raio do círculo que representa uma seção transversal do sólido.
) será o raio do círculo que representa uma seção transversal do sólido. } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: