 por Imscatman » Ter Set 27, 2011 22:56
por Imscatman » Ter Set 27, 2011 22:56
Olá.
Talvez eu esteja esquecendo algum detalhe muito idiota, mas o fato é que não estou conseguindo compreender
um passo da resolução da seguinte questão:
Prove, pela definição formal de limite, que
![\lim_{x\rightarrow{9}^{-}} \sqrt[4]{9-x} = 0 \lim_{x\rightarrow{9}^{-}} \sqrt[4]{9-x} = 0](/latexrender/pictures/b8be27c8006f5df87b787b6620ca4066.png)
Então tudo a fazer é achar

e

tal que
![9-\delta<x<9 \rightarrow \left| \sqrt[4]{9-x} \right|<\epsilon 9-\delta<x<9 \rightarrow \left| \sqrt[4]{9-x} \right|<\epsilon](/latexrender/pictures/e8585e9762d1f9833027f3505a75cce8.png)
Desenvolvendo o lado direito...
Mas neste passo eu páro.De algum modo, segundo a resolução mostrada no livro, é lícito saltar daí para:
Como?
Não entendo esse passo. Inverter

e
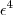
, tudo bem. Mas não entendo o que garante que
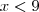
. Até onde vejo, é perfeitamente possível que
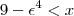
, mas que

. No entanto esse passo é necessário para concluir o exercício e provar o limite (o resto eu sei).
Obrigado pela atenção.
-

Imscatman
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mar 17, 2011 17:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qua Set 28, 2011 11:19
por LuizAquino » Qua Set 28, 2011 11:19
Imscatman escreveu:Mas neste passo eu páro.De algum modo, segundo a resolução mostrada no livro, é lícito saltar daí para:
Como?
Não entendo esse passo.
Note que deseja-se calcular o limite com x tendendo a 9 pela
esquerda (ou seja, temos
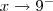
) . Dessa forma,
necessariamente os valores de x são tais que x < 9.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Imscatman » Qua Set 28, 2011 15:46
por Imscatman » Qua Set 28, 2011 15:46
Muito obrigado, professor.
Como previ, estava esquecendo um detalhe idiota, rsrsrs.
Ou melhor, idiotamente esquecendo um detalhe importante.
Mas nunca mais esqueço agora. xD
-

Imscatman
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mar 17, 2011 17:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Preciso de uma explicação passo a passo para esse exercício
por Dankaerte » Qui Ago 27, 2009 14:24
- 0 Respostas
- 2260 Exibições
- Última mensagem por Dankaerte

Qui Ago 27, 2009 14:24
Sistemas de Equações
-
- Alguém sabe como resolve (5/2)²-5(5/2)+6 passo a passo??
por Elia » Ter Jul 19, 2016 11:28
- 0 Respostas
- 2648 Exibições
- Última mensagem por Elia

Ter Jul 19, 2016 11:28
Sistemas de Equações
-
- Alguém sabe como resolve (5/2)²-5(5/2)+6 passo a passo??
por Elia » Qua Jul 20, 2016 13:57
- 2 Respostas
- 2224 Exibições
- Última mensagem por Elia

Qua Jul 20, 2016 17:51
Equações
-
- [Calculo de equação] resolução passo a passo
por leonardoandra » Seg Nov 19, 2012 20:44
- 2 Respostas
- 2372 Exibições
- Última mensagem por leonardoandra

Seg Nov 19, 2012 21:48
Álgebra Elementar
-
- [Integração por substituição] Passo a passo, por favor?
por Ronaldobb » Seg Dez 17, 2012 16:24
- 4 Respostas
- 3206 Exibições
- Última mensagem por Ronaldobb

Ter Dez 18, 2012 13:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  tal que
tal que![9-\delta<x<9 \rightarrow \left| \sqrt[4]{9-x} \right|<\epsilon 9-\delta<x<9 \rightarrow \left| \sqrt[4]{9-x} \right|<\epsilon](/latexrender/pictures/e8585e9762d1f9833027f3505a75cce8.png)
 e
e 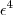 , tudo bem. Mas não entendo o que garante que
, tudo bem. Mas não entendo o que garante que 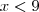 . Até onde vejo, é perfeitamente possível que
. Até onde vejo, é perfeitamente possível que 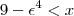 , mas que
, mas que  . No entanto esse passo é necessário para concluir o exercício e provar o limite (o resto eu sei).
. No entanto esse passo é necessário para concluir o exercício e provar o limite (o resto eu sei).
![\lim_{x\rightarrow{9}^{-}} \sqrt[4]{9-x} = 0 \lim_{x\rightarrow{9}^{-}} \sqrt[4]{9-x} = 0](/latexrender/pictures/b8be27c8006f5df87b787b6620ca4066.png)
![\left| \sqrt[4]{9-x} \right|<\epsilon \left| \sqrt[4]{9-x} \right|<\epsilon](/latexrender/pictures/03a5094edc5ec894de27daff09d59501.png)
![\sqrt[4]{9-x}<\epsilon \sqrt[4]{9-x}<\epsilon](/latexrender/pictures/cd0eeb6724997eb3d2178a17b67798cc.png)
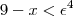
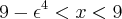

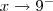 ) . Dessa forma,
) . Dessa forma, 