 por beel » Sáb Set 03, 2011 20:17
por beel » Sáb Set 03, 2011 20:17

(2x²-5x+2)/(5x²-7x-6)
Na resolução desse limite, eu teria que fatorar certo?(tirar as raizes reais do numerador e denominador)
a(X-R1)(x-R2).
Meu resultado inicial deu 3/13 , mas depois deu um numero negativo, alguem sabe quanto da?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Sáb Set 03, 2011 21:03
por Neperiano » Sáb Set 03, 2011 21:03
Ola
Você tenque fazer baskara nas duas
Fica:

Dai corta x-2 e resolve
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por beel » Sáb Set 03, 2011 21:18
por beel » Sáb Set 03, 2011 21:18
O meu resultado deu
2(x-2)(x-1/2)/5(x-2)(x + 3/5)
Depois de fazer Baskara, achar as raizes, a formula da fatoração nao seria
a(x-r1)(x-r2) ?Nao seria multiplicado pelo "a" ?
no caso 2 e 5?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Sáb Set 03, 2011 21:23
por Neperiano » Sáb Set 03, 2011 21:23
Ola
Voce corta o x-2 então fica
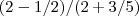
Não se esqueca de susbtituir o x, e dai faça
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por beel » Sáb Set 03, 2011 21:35
por beel » Sáb Set 03, 2011 21:35
Sim, ai daria 15/26, o que nao bate com nenhuma alternativa dentre as quais o exercicio dá.
O que eu me referi, foi se voce nao esqueceu de multiplicar, na hora de fatorar, o (x-raiz1)(x-raiz2) pelo "a" ( ax² + by + c)
Meu resultado deu 2(x-1/2)/5(x + 3/5)
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Sáb Set 03, 2011 23:08
por Neperiano » Sáb Set 03, 2011 23:08
Ola
Cara a principio não, porque na baskara tu ja usa o numero na frente do a, mas sei lá, tenta assim, se der certo
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por beel » Dom Set 04, 2011 13:50
por beel » Dom Set 04, 2011 13:50
Aparentemente deu certo, obrigada de qualquer forma.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Set 04, 2011 15:26
por LuizAquino » Dom Set 04, 2011 15:26
ObservaçãoDado um polinômio do segundo grau
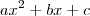
, a sua forma fatorada será
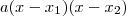
, sendo

e
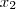
as raízes da equação
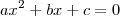
.
Por exemplo, vamos ter que:
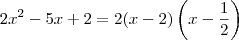
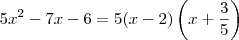
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Set 04, 2011 15:32
por beel » Dom Set 04, 2011 15:32
Exato, foi isso que eu fiz,e sobre o "a" que estava me referindo. Meu limite deu 3/13.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo de Limite] Resolução de um limite
por julianocoutinho » Seg Mai 13, 2013 01:47
- 3 Respostas
- 3333 Exibições
- Última mensagem por Man Utd

Qua Mai 15, 2013 22:26
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO
por beel » Sex Set 02, 2011 15:14
- 2 Respostas
- 1715 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:03
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO 2
por beel » Sex Set 02, 2011 17:58
- 2 Respostas
- 1713 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:03
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de Limite
por Ewerton Farias » Ter Abr 24, 2012 02:11
- 2 Respostas
- 2083 Exibições
- Última mensagem por Ewerton Farias

Sex Abr 27, 2012 17:30
Cálculo: Limites, Derivadas e Integrais
-
- resolução de limite
por luiza_ahnert » Sáb Fev 02, 2013 17:09
- 1 Respostas
- 1333 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 18:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (2x²-5x+2)/(5x²-7x-6)
(2x²-5x+2)/(5x²-7x-6)
 (2x²-5x+2)/(5x²-7x-6)
(2x²-5x+2)/(5x²-7x-6)



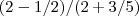




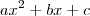 , a sua forma fatorada será
, a sua forma fatorada será 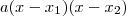 , sendo
, sendo  e
e 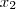 as raízes da equação
as raízes da equação 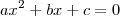 .
.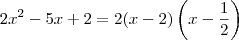
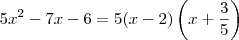


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.