 por ARCS » Ter Ago 23, 2011 18:15
por ARCS » Ter Ago 23, 2011 18:15
Sempre que queremos calcular a integral da secante temos que multliplicar a secante por (secx+tgx) / (secx+tgx). Existe alguma forma de deduzir este fator ou terei que memoriza-lo mesmo?
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Neperiano » Ter Ago 23, 2011 19:36
por Neperiano » Ter Ago 23, 2011 19:36
Ola
Você pode transforma-la em 1/cos x, mas acho que isso naum ajuda muito
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Ter Ago 23, 2011 23:02
por LuizAquino » Ter Ago 23, 2011 23:02
ARCS escreveu:Sempre que queremos calcular a integral da secante temos que multliplicar a secante por (secx+tgx) / (secx+tgx). Existe alguma forma de deduzir este fator ou terei que memoriza-lo mesmo?
Essa estratégia, bem esperta, é realizada já pensando na utilização da técnica de substituição no passo seguinte.
A forma de "deduzi-la" seria exatamente pensando na questão: o que devo multiplicar para depois poder usar a técnica de substituição?
Comparado a quem teve pela primeira vez essa ideia, que foi bastante criativa, o nosso trabalho é bem simples: aprendê-la (que é diferente de decorá-la).
Neperiano escreveu:Você pode transforma-la em 1/cos x, mas acho que isso naum ajuda muito
Sim, ajuda.
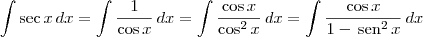
Fazendo a substituição
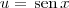
e
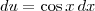
, obtemos
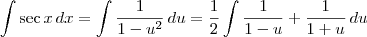
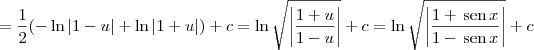
Para deixar a família de primitivas no formato canônico, faremos o desenvolvimento abaixo.
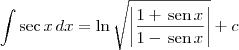
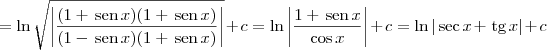
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada de secante.
por Sobreira » Ter Nov 27, 2012 16:38
- 3 Respostas
- 2958 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 22:27
Cálculo: Limites, Derivadas e Integrais
-
- Demonstração- secante
 por mathsoliver » Seg Abr 13, 2015 12:32
por mathsoliver » Seg Abr 13, 2015 12:32
- 1 Respostas
- 1762 Exibições
- Última mensagem por Cleyson007

Seg Abr 13, 2015 16:51
Equações
-
- seno e secante negativa
por Apotema » Seg Nov 23, 2009 14:36
- 2 Respostas
- 1993 Exibições
- Última mensagem por Apotema

Qua Nov 25, 2009 16:54
Trigonometria
-
- Função Secante e Cossecante
por gustavoluiss » Qui Jul 14, 2011 20:42
- 11 Respostas
- 5519 Exibições
- Última mensagem por gustavoluiss

Sáb Jul 16, 2011 15:19
Trigonometria
-
- Declive da reta secante
por joaofonseca » Ter Nov 08, 2011 12:04
- 3 Respostas
- 4712 Exibições
- Última mensagem por LuizAquino

Sex Nov 11, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




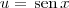 e
e 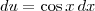 , obtemos
, obtemos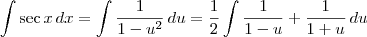
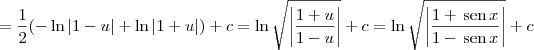
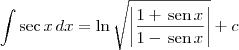
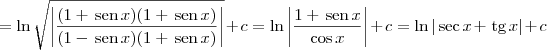

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.