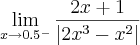
aplicando os principios de módulo aí (até onde eu sei) fica duas possibilidades...
1.
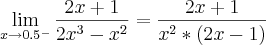
2.
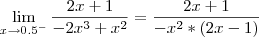
Daí pra frente não consigo fazer mais nada já que não consigo eliminar termos nessas equações...

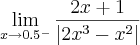
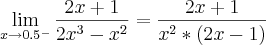
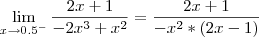

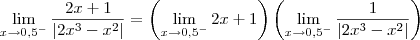
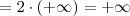


killerkill escreveu:Pois é, mais no gabarito do livro a resposta é -1/2
=/


killerkill escreveu:Livro do Stewart só que o sexta ediçao ( o ultimo lançado) Volume 1 - Exercicios 2.3 questao 29 - pagina 96
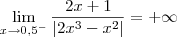

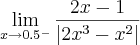

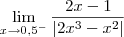 , então o resultado é -4.
, então o resultado é -4.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes