Boa noite, Alexandre.
Vou dar a ideia de como eu pensaria nesta questão e quero ver se você chega a mesma conclusão que eu:
Se imaginarmos os números reais como uma reta, teremos que cada ponto que forma esta reta são os números reais. Alguns pontos são os racionais e outros pontos são os irracionais. A união dos dois conjuntos de pontos formará a reta (
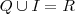
). Se retirarmos, por exemplo, os números irracionais será possível observar alguns "buracos" nesta reta. O restante que permanece na reta são os números racionais.
Um esboço disso seria:
______ _______ ____ _ ___ ____ _____________ ___ _ ____________ _ _____ ______________ _ _ ____
Colocando este esboço num sistema de coordenadas xy e esta reta com buracos sobre o eixo x, representaria parte do nosso problema em questão, pois para todo número racional, temos que a função vale 0. Falta saber o que fazer com esses pontos que retiramos.
Lembre-se que para uma função ser contínua ela não tem "buracos", ou seja, temos que desenhar toda a função "sem tirar o lápis do papel".
Então, quais os valores que esses pontos com "buracos" devem assumir para que esses "buracos" não existam mais sobre esta reta?




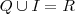 ). Se retirarmos, por exemplo, os números irracionais será possível observar alguns "buracos" nesta reta. O restante que permanece na reta são os números racionais.
). Se retirarmos, por exemplo, os números irracionais será possível observar alguns "buracos" nesta reta. O restante que permanece na reta são os números racionais. 



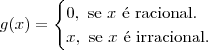
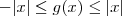 .
.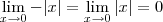 , pelo Teorema do Sanduíche segue que
, pelo Teorema do Sanduíche segue que 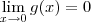 . Por outro lado, sabemos que g(0) = 0.
. Por outro lado, sabemos que g(0) = 0. 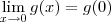 . Isso é o mesmo que dizer que g é contínua em x = 0.
. Isso é o mesmo que dizer que g é contínua em x = 0.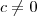 e qualquer real
e qualquer real 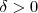 . No intervalo
. No intervalo 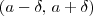 existem infinitos racionais e infinitos irracionais.
existem infinitos racionais e infinitos irracionais. e
e 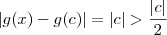 .
.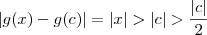 .
.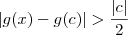 .
.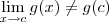 . Isso é o mesmo que dizer que g não é contínua em x = c (lembrando-se que tomamos qualquer real
. Isso é o mesmo que dizer que g não é contínua em x = c (lembrando-se que tomamos qualquer real 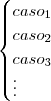
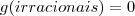 .
.