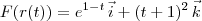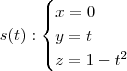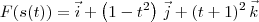por Bruhh » Ter Jul 05, 2011 16:55
por Bruhh » Ter Jul 05, 2011 16:55
Ol Boa Tarde
Estou com muita dificuldade de resolver um problema que envolve cálculo de trabalho através
da integral de linha.Necessito de ajuda cpm certa urgência por isso se alguém puder, preciso de
ajuda logo.Abaixo o problema minhas dúvidas e resoluções:
Seja a força definida pelo campo
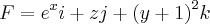
Determine o trabalho realizado por esta, para deslocar uma partícula segundo o caminho.
(1,0,0)...(0,1,0) ...(0,0,1)
*Figura em anexo
Parametrizando o caminho 1:
x= 1- t
y=t
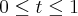
Assim, para o caminho C1
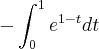
O problema é no segundo caminho onde z varia com uma função.Não sei como faço para achar a parametrização de y e z.
Alguém pode me ajudar, por favor?
Muito Obrigada
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por LuizAquino » Ter Jul 05, 2011 19:10
por LuizAquino » Ter Jul 05, 2011 19:10
Primeiro, note que uma parametrização para o caminho 1 é:
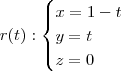
Desse modo, a função
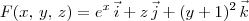
pelo caminho 1 pode ser reescrita como:
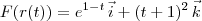
Já o caminho 2 tem uma parametrização dada por:
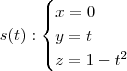
Desse modo, a função
F pelo caminho 2 pode ser reescrita como:
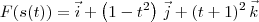
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo de notação vetorial e trabalho usando intg. de linha
por Fernandobertolaccini » Ter Fev 03, 2015 12:43
- 1 Respostas
- 1648 Exibições
- Última mensagem por Russman

Ter Fev 03, 2015 19:07
Cálculo: Limites, Derivadas e Integrais
-
- Integral de linha - 2
por DanielFerreira » Dom Jun 03, 2012 16:14
- 2 Respostas
- 2975 Exibições
- Última mensagem por DanielFerreira

Dom Jun 03, 2012 19:14
Cálculo: Limites, Derivadas e Integrais
-
- Integral de linha
por calc3 » Dom Jun 07, 2015 11:43
- 0 Respostas
- 3228 Exibições
- Última mensagem por calc3

Dom Jun 07, 2015 11:43
Cálculo: Limites, Derivadas e Integrais
-
- [Integral de Linha] Teoria
por Claudin » Qui Jul 25, 2013 23:47
- 0 Respostas
- 2100 Exibições
- Última mensagem por Claudin

Qui Jul 25, 2013 23:47
Cálculo: Limites, Derivadas e Integrais
-
- [Integral de linha] problema
 por Ahoush123 » Sáb Nov 28, 2015 15:20
por Ahoush123 » Sáb Nov 28, 2015 15:20
- 0 Respostas
- 2833 Exibições
- Última mensagem por Ahoush123

Sáb Nov 28, 2015 15:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
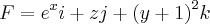
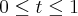
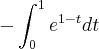


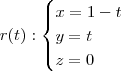
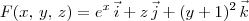 pelo caminho 1 pode ser reescrita como:
pelo caminho 1 pode ser reescrita como: