 por Jaison Werner » Sáb Mai 21, 2011 10:45
por Jaison Werner » Sáb Mai 21, 2011 10:45
CALCULE PELA REGRA DE SIMPSON O VALOR:
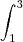
x
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
, com n = 4.
-
Jaison Werner
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Sex Abr 23, 2010 20:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: cursando
 por Jaison Werner » Sáb Mai 21, 2011 10:58
por Jaison Werner » Sáb Mai 21, 2011 10:58
-
Jaison Werner
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Sex Abr 23, 2010 20:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: cursando
 por LuizAquino » Dom Mai 22, 2011 19:00
por LuizAquino » Dom Mai 22, 2011 19:00
Você deseja usar o Regra de Simpson Composta.
Dado
n par,
h = (
b -
a)/
n e
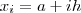
, a regra nos fornece:
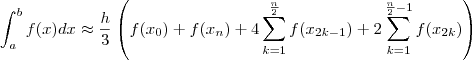
No exercício, temos

,
a = 1,
b = 3,
n = 4,
h = 1/2 e

:


Agora, basta fazer os cálculos.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por hugo82 » Seg Mai 30, 2011 16:31
por hugo82 » Seg Mai 30, 2011 16:31
Olá, estou com dificuldades em integrais deste tipo:
integral x^2 / (5-(x^6)) dx
-
hugo82
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mai 30, 2011 16:07
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engenharia
- Andamento: cursando
 por stuart clark » Seg Mai 30, 2011 17:58
por stuart clark » Seg Mai 30, 2011 17:58
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por hugo82 » Seg Mai 30, 2011 18:50
por hugo82 » Seg Mai 30, 2011 18:50
Não estou conseguindo resolver este integral:
?((2^?x)/?x)
-
hugo82
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mai 30, 2011 16:07
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engenharia
- Andamento: cursando
 por demolot » Ter Mai 31, 2011 00:48
por demolot » Ter Mai 31, 2011 00:48
nao estou a perceber se é
![\int_{}^{}\frac{{\sqrt[]{x}}^{2}}{\sqrt[]{x}} \int_{}^{}\frac{{\sqrt[]{x}}^{2}}{\sqrt[]{x}}](/latexrender/pictures/af733f084743d384b3c6e8b5e940e648.png)
ou
![\int_{}^{}\frac{{2}^{\sqrt[]{x}}}{\sqrt[]{x}} \int_{}^{}\frac{{2}^{\sqrt[]{x}}}{\sqrt[]{x}}](/latexrender/pictures/c744ec1feedc0a63066d9299735c5cb4.png)
-
demolot
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Dez 11, 2010 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Informatica
- Andamento: cursando
 por stuart clark » Ter Mai 31, 2011 02:05
por stuart clark » Ter Mai 31, 2011 02:05
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por hugo82 » Ter Mai 31, 2011 08:37
por hugo82 » Ter Mai 31, 2011 08:37
Não estou conseguindo concluir este integral:
![\int_{\frac{x}{\sqrt[]{(1+x^2+\sqrt[]{(1+x^2)^3}}}}^{} \int_{\frac{x}{\sqrt[]{(1+x^2+\sqrt[]{(1+x^2)^3}}}}^{}](/latexrender/pictures/4aebd00e316798afbdf0b7e1c86e8e1d.png)
-
hugo82
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mai 30, 2011 16:07
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engenharia
- Andamento: cursando
 por stuart clark » Ter Mai 31, 2011 14:17
por stuart clark » Ter Mai 31, 2011 14:17
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8866 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2819 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2447 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2534 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2141 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
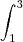 x
x ![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) , com n = 4.
, com n = 4.
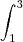 x
x ![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) , com n = 4.
, com n = 4.
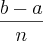
 .(
.(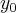
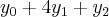
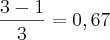
![{y}_{0}= 1.\sqrt[]{1 = 1} {y}_{0}= 1.\sqrt[]{1 = 1}](/latexrender/pictures/cee8c12254ac02930c675a6ab1f23cc6.png)
![{y}_{1}=1,5.\sqrt[]{1,5}= 1,84 {y}_{1}=1,5.\sqrt[]{1,5}= 1,84](/latexrender/pictures/749205e1c0d21bb8654645039b0d43bb.png)
![{y}_{2}= 2.\sqrt[]{2}= 2.83 {y}_{2}= 2.\sqrt[]{2}= 2.83](/latexrender/pictures/df6f770b386cb837fbabdde350f72a6e.png)
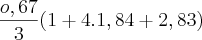

![{E}_{t}= -\frac{0,67}{90}. 0,56
[tex]{E}_{t}=- 0,004 {E}_{t}= -\frac{0,67}{90}. 0,56
[tex]{E}_{t}=- 0,004](/latexrender/pictures/b32f8dcdc2c2236e947a47b0b2f30058.png)

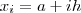 , a regra nos fornece:
, a regra nos fornece: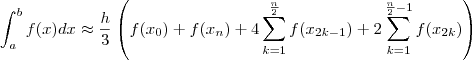
 , a = 1, b = 3, n = 4, h = 1/2 e
, a = 1, b = 3, n = 4, h = 1/2 e  :
:




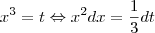
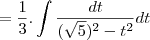
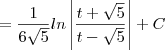


![\int_{}^{}\frac{{\sqrt[]{x}}^{2}}{\sqrt[]{x}} \int_{}^{}\frac{{\sqrt[]{x}}^{2}}{\sqrt[]{x}}](/latexrender/pictures/af733f084743d384b3c6e8b5e940e648.png)
![\int_{}^{}\frac{{2}^{\sqrt[]{x}}}{\sqrt[]{x}} \int_{}^{}\frac{{2}^{\sqrt[]{x}}}{\sqrt[]{x}}](/latexrender/pictures/c744ec1feedc0a63066d9299735c5cb4.png)


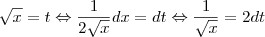


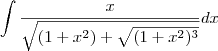
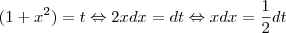
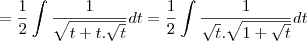
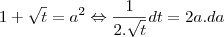


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)