Primeiro gostaria de parabenizá-los pela iniciativa de dividir dúvidas e sabedorias. Só olhando os tópicos já me ajudou muito, mas uma dúvida permanece, referente ao exercício:
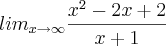
Sendo que o numerador todo é uma raiz, ou seja, raiz quadrada de x^2-2x+2. (não consegui colocar raiz na fórmula).
Sei que devo colocar a maior potência de x em evidência, e depois o x sai da raiz e fica como módulo. A questão é, o fato do x estar em módulo isso altera em alguma coisa o desenvolvimento? Agarrei aí e não consigo continuar, pois o x no numerador fica |x|, mas no denominador fica somente x. Fiquei na dúvida se posso cortar ou não.
E caso o limite fosse: x tende a menos infinito, com o restante igual?


![\lim_{x\rightarrow \infty}\frac{\sqrt[]{{x}^{2}-2x+2}}{x+1} \lim_{x\rightarrow \infty}\frac{\sqrt[]{{x}^{2}-2x+2}}{x+1}](/latexrender/pictures/b99c1b06f580fdac663923cc9cd17114.png)
![\lim_{x\rightarrow \infty}\frac{\sqrt[]{{x}^{2}-2x+2}}{x+1}.\frac{\sqrt[]{{x}^{2}-2x+2}}{\sqrt[]{{x}^{2}-2x+2}} \lim_{x\rightarrow \infty}\frac{\sqrt[]{{x}^{2}-2x+2}}{x+1}.\frac{\sqrt[]{{x}^{2}-2x+2}}{\sqrt[]{{x}^{2}-2x+2}}](/latexrender/pictures/59bb0ed05e5e7afd9c3a8be825612901.png)


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)