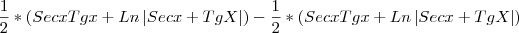por monicaoliveira » Ter Abr 19, 2011 11:43
por monicaoliveira » Ter Abr 19, 2011 11:43
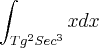
Pessoal, tg^2 x +1=Sec^2
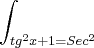
Eu substitui e deu a soma de duas integrais mais complicadas
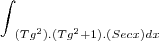
Aí me compliquei...
O livro só mostra a estratégia para a potência de secacnte par e para a potencia de tangente ímpar.
Mas daí eu não sei sair, preciso de ajuda urgente por favor!
-
monicaoliveira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Abr 19, 2011 11:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: cursando
 por LuizAquino » Ter Abr 19, 2011 14:08
por LuizAquino » Ter Abr 19, 2011 14:08
Usando a identidade
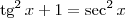
, temos que:
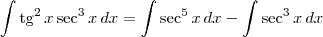
.
Agora, aplique a fórmula de recorrência:
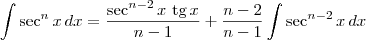
, para

, com
n natural.
Vale lembrar que no caso
n=1 temos que:
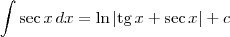
.
ObservaçãoVocê pode encontrar a demonstração dessa fórmula de recorrência em alguns livros de Cálculo. Por exemplo, no livro "Um Curso de Cálculo" (vol. 1) de Guidorizzi.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por monicaoliveira » Ter Abr 19, 2011 16:13
por monicaoliveira » Ter Abr 19, 2011 16:13
Muito obrigada Luiz, mas eu não sei usar a fórmula de recorrência.
MAs sei a resposta de
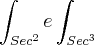
Posso escrever dessa forma a resposta?
Tg*
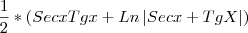
-
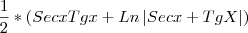
-
monicaoliveira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Abr 19, 2011 11:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: cursando
 por LuizAquino » Ter Abr 19, 2011 18:44
por LuizAquino » Ter Abr 19, 2011 18:44
monicaoliveira escreveu:Muito obrigada Luiz, mas eu não sei usar a fórmula de recorrência.
Se você não sabe usá-la, então eu recomendo que estude um pouco mais. Ela será importante para resolver exercícios como este.
Veja um exemplo:
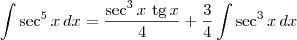
.
Agora, você tem que continuar a resolução aplicando a fórmula de recorrência para
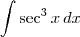
.
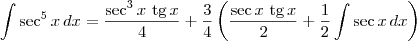
.
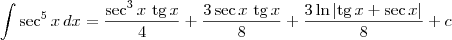
.
monicaoliveira escreveu:MAs sei a resposta de
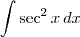
e
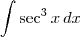
.
Posso escrever dessa forma a resposta?
Tg*
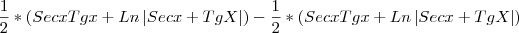
Esta resposta não faz sentido.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4623 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4591 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4350 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2853 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2882 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
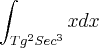
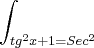
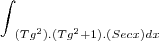


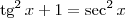 , temos que:
, temos que: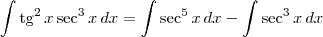 .
.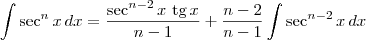 , para
, para  , com
, com 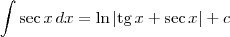 .
.
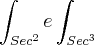
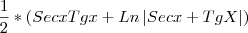 -
- 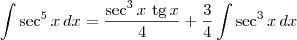 .
.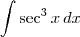 .
.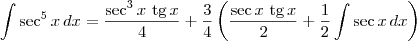 .
.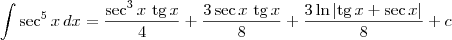 .
.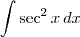 e
e 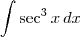 .
.