Primeiro, sempre organize o seu texto. Do jeito que está escrito o exercício não está fazendo sentido.
Ao que parece, o que se quer é determinar a
Série de Fourier para a função 2pi periódica dada por f(x)=cosh(x)senh(x) quando x pertence a (-pi, pi).
Primeiro, lembre-se que da definição de
seno hiperbólico e
cosseno hiperbólico, temos que a função f é equivalente a
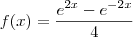
no intervalo dado.
Sabemos que a
Série de Fourier para uma função 2pi periódica que é integrável em [-pi, pi] é dada por
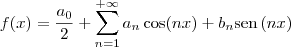
,
sendo que
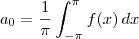
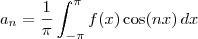
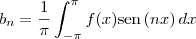
com n=1, 2, 3, ...
Utilizando as propriedades da
Série de Fourier, sabemos que para uma função 2pi periódica ímpar, temos que
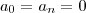
. Portanto, temos que calcular apenas
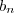
.
Nesse exercício, usando integração por partes, teremos que
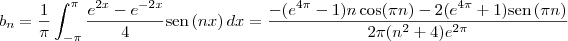
Note que para qualquer n natural, temos que
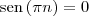
.
Por outro lado, se n é par, então
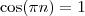
; se n é ímpar, então
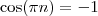
. Desse modo,
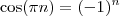
, com n natural.
Sendo assim, teremos que
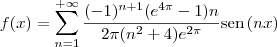
A figura a seguir ilustra a aproximação de f no intervalo (-pi, pi) com k termos:
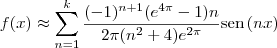
, com k=1, 2, 3, ..., 32.
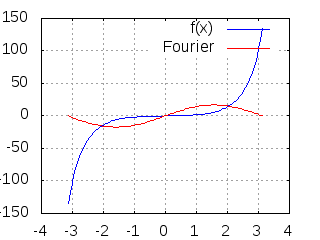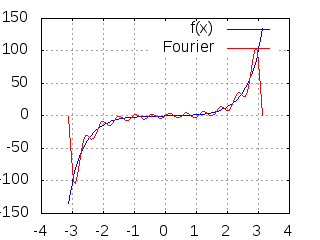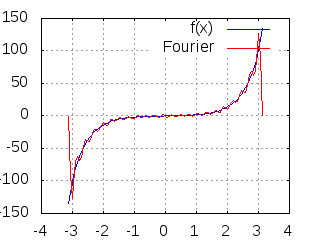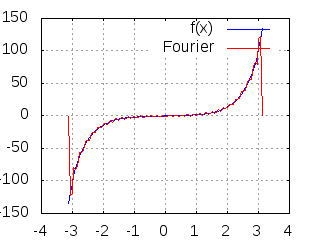
- fourier.gif (114.99 KiB) Exibido 2187 vezes



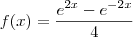 no intervalo dado.
no intervalo dado.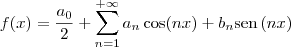 ,
,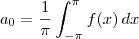
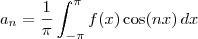
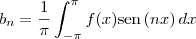
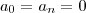 . Portanto, temos que calcular apenas
. Portanto, temos que calcular apenas 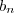 .
.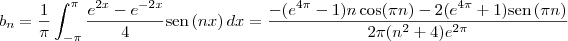
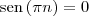 .
.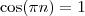 ; se n é ímpar, então
; se n é ímpar, então 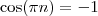 . Desse modo,
. Desse modo, 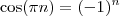 , com n natural.
, com n natural.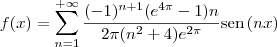
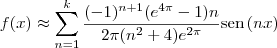 , com k=1, 2, 3, ..., 32.
, com k=1, 2, 3, ..., 32.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)