 por Kelvin Brayan » Qui Mar 10, 2011 11:59
por Kelvin Brayan » Qui Mar 10, 2011 11:59
01.(UFC) Sejam x e y números reais, tais que
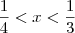
;
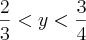
e A= 3x-2y
Então, é
CORRETO afirmar que:
A)
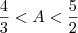
B)
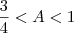
C)
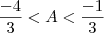
D)
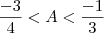
E)
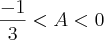
Segundo o gabarito, a resposta certa é a letra D. No entanto, eu não sei nem como começa para resolvê-la.
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por Elcioschin » Qui Mar 10, 2011 12:37
por Elcioschin » Qui Mar 10, 2011 12:37
Existem 4 combinações possíveis:
x = 1/4, y = 2/3 ----> A = 3*(1/4) - 2*(2/3) ----> A = - 7/12
x = 1/4, y = 3/4 ----> A = 3*(1/4) - 2*(3/4) ----> A = - 3/4
x = 1/3, y = 2/3 ----> A = 3*(1/3) - 2*(2/3) ----> A = - 1/3
x = 1/3, y = 3/4 ----> A = 3*(1/3) - 2*(3/4) ----> A = - 1/2
Menor valor = - 3/4
Maior valor = - 1/3
- 3/4 < A < - 1/3 ----> D
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Kelvin Brayan » Qui Mar 10, 2011 15:47
por Kelvin Brayan » Qui Mar 10, 2011 15:47
Valeu !!!
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por LuizAquino » Qui Mar 10, 2011 16:42
por LuizAquino » Qui Mar 10, 2011 16:42
Uma outra estratégia de resolução é usar os conhecimentos sobre inequações.
Vamos precisar de duas propriedades:
(i) se
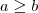
, então
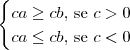
.
(ii) Se
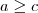
e
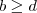
, então
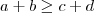
.
Nós temos
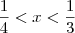
. Multiplicando-se toda a inequação por 3, obtemos
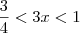
.
Por outro lado, temos
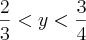
. Multiplicando-se toda a inequação por -2, obtemos
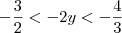
.
Somando-se as inequações, obtemos
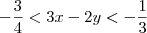
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10976 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15120 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5035 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4803 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
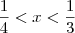 ;
; 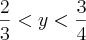 e A= 3x-2y
e A= 3x-2y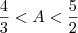
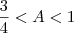
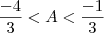
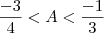
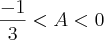

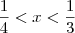 ;
; 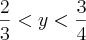 e A= 3x-2y
e A= 3x-2y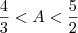
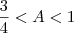
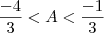
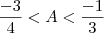
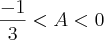



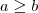 , então
, então 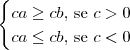 .
.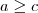 e
e 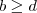 , então
, então 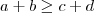 .
.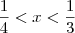 . Multiplicando-se toda a inequação por 3, obtemos
. Multiplicando-se toda a inequação por 3, obtemos 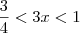 .
.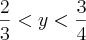 . Multiplicando-se toda a inequação por -2, obtemos
. Multiplicando-se toda a inequação por -2, obtemos 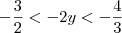 .
.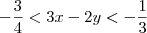 .
.

 .
.
 :
: