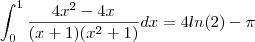por OtavioBonassi » Sáb Jan 15, 2011 14:57
por OtavioBonassi » Sáb Jan 15, 2011 14:57
"O valor de
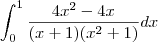
é : "
Galera, tentei fazer essa integral por aquele método de divisao de polinomios ,e fazer A + B + C etc etc mas não deu certo nao ,alguem tem alguma idéia ?
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por MarceloFantini » Sáb Jan 15, 2011 19:55
por MarceloFantini » Sáb Jan 15, 2011 19:55
Como você fez a divisão? Talvez tenha feito errado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por OtavioBonassi » Dom Jan 16, 2011 01:15
por OtavioBonassi » Dom Jan 16, 2011 01:15
Então Fantini ,mas acho que nao é por esse jeito que eu tava fazendo não cara, sei lá
porque a resposta pro exercicio é 4ln2 - pi ,da onde raios eu vou tirar um pi fazendo por esse método ?! Seguindo esse caminho ai eu vou cair em umas integrais de polinomios, sem idéia de como chegar nesse resultado
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por MarceloFantini » Dom Jan 16, 2011 14:55
por MarceloFantini » Dom Jan 16, 2011 14:55
Ainda não consegui resolver. Curiosidade: de onde tirou essa integral?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por OtavioBonassi » Dom Jan 16, 2011 16:40
por OtavioBonassi » Dom Jan 16, 2011 16:40
Tirei da prova de transferência USP 2009
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Santa Lucci » Qui Fev 03, 2011 15:37
por Santa Lucci » Qui Fev 03, 2011 15:37
Olá, tudo bom? Segue a minha resolução, perdoe-me pelos possíveis erros.
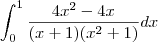
Usando o método das frações parciais...
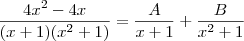
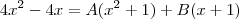
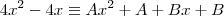
Montando e resolvendo um sistema de equações, descobrimos que

e
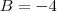
Então,
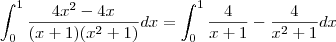
Como a integral indefinida de
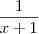
é

; e a de
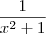
é
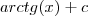
, temos (já substituindo os extremos de integração),
![\int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)] \int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)]](/latexrender/pictures/98b5dd7dbc6c2cc0d1686e9a383a7925.png)
Portanto,
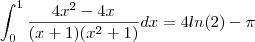
Att,
Santa Lucci.
-
Santa Lucci
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jan 02, 2011 19:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: cursando
 por Santa Lucci » Qui Fev 03, 2011 15:38
por Santa Lucci » Qui Fev 03, 2011 15:38
Olá, tudo bom? Segue a minha resolução, perdoe-me pelos possíveis erros.
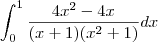
Usando o método das frações parciais...
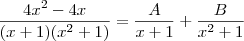
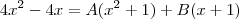
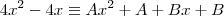
Montando e resolvendo um sistema de equações, descobrimos que

e
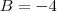
Então,
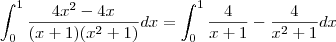
Como a integral indefinida de
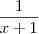
é

; e a de
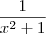
é
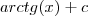
, temos (já substituindo os extremos de integração),
![\int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)] \int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)]](/latexrender/pictures/98b5dd7dbc6c2cc0d1686e9a383a7925.png)
Portanto,
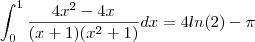
Att,
Santa Lucci.
-
Santa Lucci
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jan 02, 2011 19:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão estranha
por Kelvin Brayan » Ter Abr 19, 2011 13:35
- 2 Respostas
- 2114 Exibições
- Última mensagem por Kelvin Brayan

Ter Abr 19, 2011 14:35
Álgebra Elementar
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4623 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4590 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4348 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2848 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
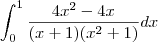 é : "
é : " 
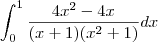 é : "
é : " 





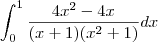
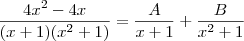
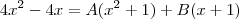
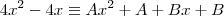
 e
e 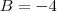
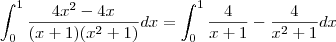
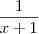 é
é  ; e a de
; e a de 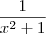 é
é 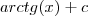 , temos (já substituindo os extremos de integração),
, temos (já substituindo os extremos de integração),![\int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)] \int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)]](/latexrender/pictures/98b5dd7dbc6c2cc0d1686e9a383a7925.png)
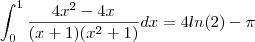

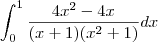
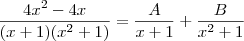
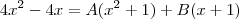
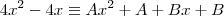
 e
e 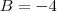
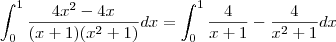
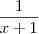 é
é  ; e a de
; e a de 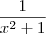 é
é 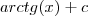 , temos (já substituindo os extremos de integração),
, temos (já substituindo os extremos de integração),![\int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)] \int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)]](/latexrender/pictures/98b5dd7dbc6c2cc0d1686e9a383a7925.png)