Olá Elcio!
Você pode enviar sim o seu desenvolvimento, inclusive recomendo.
Lembrando que apenas precisamos do "cálculo" para obtermos a área
sob a curva

, pois podemos obter a área sob a curva

, considerando o trapézio retângulo delimitado, veja:
E com a integral, subtraímos esta outra área:
Sendo assim, a diferença é a área procurada:
É claro que também podemos calcular a primeira área com integral, não há problema.
E como as duas funções são integráveis no intervalo, a integral da diferença é igual à diferença das integrais.
Portanto, as alternativas para obtermos a área

pedida são:
-calcular a área
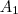
do trapézio (apenas por geometria plana) e
subtrair do resultado o valor de

-analogamente, calcular a diferença:
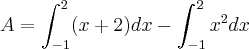
-ou ainda, utilizando a propriedade da integral, calcular diretamente:
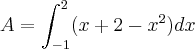
Cuidado com os sinais ao utilizar o Teorema Fundamental do Cálculo.
Aguardo suas tentativas.
Até mais!


 e
e  .
.
 pedida são:
pedida são: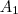 do trapézio (apenas por geometria plana) e
do trapézio (apenas por geometria plana) e 
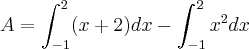
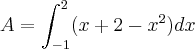
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
