se alguém puder me ajudar com esse problema de taxas de variação relacionadas, desde já agradeço. Abaixo segue o enunciado:
Uma piscina tem 24m de comprimento e seus extremos são trapézios isósceles com altura de 6m, uma base menor de 6m e uma base maior de 8m. A água está sendo bombeada para a piscina à razão de 10m³/min. Com que velocidade o nível de água está subindo quando a profundidade da água é de 2m ?
Resposta:
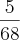m/min.Eu calculei a área do trapézio quando a profundidade da água é igual a 2m e cheguei no valor 10,008m². Para achar o Volume, multipliquei a área pelo comprimento da piscina e cheguei ao valor 240,192m³.
Porém, estou tendo dificuldades para interpretar o problema e aplicar a regra da cadeia.
Acredito que a informação dada no problema é que
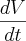=10m³/min.O problema está pedindo a informação da velocidade
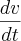quando a profundidade da água for igual a 2m.Cheguei até o seguinte ponto:
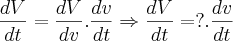
Me corrijam se eu interpretei errado.
Obrigado.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)