 por MJC » Ter Mai 06, 2008 12:41
por MJC » Ter Mai 06, 2008 12:41
Sou aluno de administração e estou cursando a disciplina de métodos determinísticos. Infelizmente, tenho muita dificuldade com as questões que envolvem
limites e freqüentemente deparo-me com indeterminações. Gostaria que, se fosse possível, algum participante do fórum me auxiliasse em alguma questões.
1) lim f(x), quando f(x)={2x+3, se x<1; 14, se x=1; 7-2x, se x>1}
x -> 1
2) lim x³-2x+20
x->

______________________
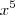
+ 6x³ +9
Espero que tenha ficado claro a segunda questão, pois não tenho prática em utilizar LaTex via BBCode e por isso acabou saindo uma fórmula meio truncada, mas seria na realidade x quando se aproxima do infinito e no 1°termo do denominador x elevada a quinta potência. Desde já agradeço a tenção dispensada
-
MJC
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mai 06, 2008 10:39
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Mai 06, 2008 15:10
por admin » Ter Mai 06, 2008 15:10
Olá, seja bem-vindo!
Favor conferir se as questões estão como você pretendia escrever.
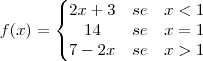
Neste caso, é importante fazer o gráfico para visualizar a idéia, veja:
Para que exista o
limite da função

, os
limites laterais devem ser iguais.
Aqui, tendendo pela esquerda:
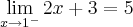
Tendendo pela direita:

Note que
o limite de

é igual a 5, com x tendendo a 1.
O que não significa que a função

assuma o valor 5 quando

, tanto é que

.
Neste outro prolema,
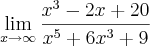
Dividindo o numerador e denominador por

, temos:
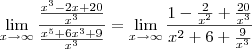
Como agora não há uma indeterminação, aplique as propriedades de
limites:

Espero ter ajudado.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por MJC » Ter Mai 06, 2008 15:58
por MJC » Ter Mai 06, 2008 15:58
Fico Muito agradecido pela ajuda. Poderia recomendar-me algum livro sobre a matéria que venha acompanhado de questões resolvidas?
-
MJC
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mai 06, 2008 10:39
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Mai 06, 2008 16:08
por admin » Ter Mai 06, 2008 16:08
Olá.
Recomendo não só o primeiro livro de nossa
bibliografia (Stewart), mas qualquer outro livro de cálculo I, por exemplo, o volume 1 do Guidorizzi.
Além da leitura deste tópico com informações sobre o e-cálculo, com teoria, exemplos e exercícios:
viewtopic.php?f=120&t=115#p186
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por MJC » Ter Mai 06, 2008 17:28
por MJC » Ter Mai 06, 2008 17:28
Caro Fábio, desculpe-me pelo abuso, mas existe outro tópico relacionado que me funde a cabeça. Assíntotas. Primeiro, gostaria de entender onde posso usar estes conceitos em administração? Se puderes me ajudar ficaria feliz, pois não consigo visualizar qualquer utilidade.
Duas questões que me apresentaram no curso: Determinar assíntotas verticais e horizontais, caso existam, das funções:
1) f(x)= 3/(x-2)²
2)g(x)= 2x-6/x+1
-
MJC
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mai 06, 2008 10:39
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Mai 06, 2008 19:05
por admin » Ter Mai 06, 2008 19:05
Olá.
Sobre as aplicações em administração, não sou habilitado para dizer, mas vale comentar que o estudo da matemática em si não se restringe às aplicações. De qualquer forma, posso citar curvas de demanda como exemplo, onde se faz uso de
integrais. E ao falar de cálculo:
limites e assíntotas são exemplos de pré-requisitos! Mesmo que por ora você não encontre aplicações relacionadas às assíntotas, certamente encontrará para
derivadas e
integrais.
Para seu estudo de assíntotas, pense inicialmene em uma hipérbole, por exemplo a função

.
Há uma assíntota vertical e outra horizontal.
Quanto x tende a zero, o valores de y ficam arbitrariamente grandes (em módulo).
A reta

é a assíntota vertical que nunca e tocada pela hipérbole.
Por outro lado, quanto tornamos x arbitrariamente grande (em módulo), notamos que o valor da função tende a zero, os valores de y ficam arbitrariamente pequenos (em módulo).
A reta

é a assíntota horizontal que também nunca é tocada pela hipérbole.
Considero que este seja o exemplo mais didático para extrair este entendimento. Pense com o gráfico.
Para descobrir as assíntotas, você precisará utilizar
limites.
Em geral, a assíntota vertical é determinada por alguma restrição no denominador por ser zero.
A assíntota horizontal obtemos analisando o
limite da função quando
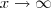
.
Veja, no segundo exercício que você enviou, vimos que o
limite da função quando
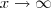
é zero (o
limite é 0).
Ou seja, a reta

é a assíntota horizontal.
Sugiro ler a teoria no livro do Stewart sobre
limites no infinito, assíntotas horizontais e verticais.
Se necessário, comente após suas tentativas.
Espero ter ajudado e bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Ter Mai 06, 2008 21:06
por admin » Ter Mai 06, 2008 21:06
Olá.
Sugestões para os exercícios de determinação das assíntotas:
1)
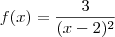
Pense na assíntota vertical como um valor da abscissa (eixo x) onde a função não está definida.
Neste caso, localize o problema do denominador (não pode ser zero).
Pergunte-se: qual valor de x anularia o denominador?
A assíntota vertical é a reta sobre este valor, perpendicular ao eixo x.
Para a assíntota horizontal, calcule:
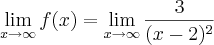
2)

Analogamente neste caso.
Para a assíntota vertical, pergunte-se: qual denominador tem restrição? Em qual valor de x?
Para a assíntota horizontal, calcule o
limite:
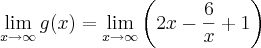
Neste caso,

, o que indica não existir assíntota horizontal (pense no gráfico).
O mesmo vale para
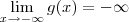
.
Em palavras, esta idéia pode ser dita assim: quando aumentamos x arbitrariamente, em módulo, a função g também cresce arbitrariamente (em módulo), ou seja, sem limitações como aconteceria se houvesse assíntota horizontal.
Acho que a partir daqui você já deve perceber que as assíntotas estão associadas com as limitações das funções consideradas. Talvez esta idéia facilite suas reflexões sobre aplicações em sua área.
Aguardo sua interação. Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por MJC » Qua Mai 07, 2008 00:19
por MJC » Qua Mai 07, 2008 00:19
Um colega de curso está estudando pelo seguinte título: Matemática para Administração, autor: Hamilton Luiz Guidorizzi, como o sobrenome é o mesmo do que você citou, talvez você tenha referências sobre a obra.Percebo que ele está muito mais afeito a matéria do que eu, o que também não é lá grande coisa, pois estou com sérias dificuldades. Sendo mais claro, Estudo em Universidade Federal do RJ que adota uma literatura própria, organizada pelos professores,com uma abordagem de conhecimento mais avançada do que possuo. Neste bimestre iniciamos com funçoes exponenciais e logarítmicas, depois passamos a noção intutiva de limite, limites de funções e suas propriedades, limites laterais, limites envolvendo infinito e em algum momento eu perdi o fio da meada, algo como se eu tivesse perdido alguma aula, algo que não aconteceu. Começo a perceber que necessitarei de um esforço imenso para compreender a matéria. Fico agradecido a você, pois sua explicações tem me valido mais do que 100 páginas de livro. Recomendo inclusive que pense sériamente em desenvolver seu lado editorial, pois nesta área sempre encontramos vazios didáticos em diversas obras. De quaquer modo, continuarei frequentando o site, pois muito tem me servido para a rotina de estudos. Abraço.
-
MJC
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mai 06, 2008 10:39
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qua Mai 07, 2008 00:58
por admin » Qua Mai 07, 2008 00:58
Olá, boa noite.
O autor é sim o mesmo, mas eu não tenho e ainda não conheço este volume para administração.
Considerando a boa qualidade das obras em cálculo, mesmo sem conhecer, acredito que seria bem interessante para seu caso.
Em meu curso também tive sérias dificuldades, considerando o nível cobrado. Acho que a grande vantagem deste fato comum a nós e certamente a muitos outros alunos de universidades públicas, é que aperfeiçoamos o modo de aprender, mais independente de professores ou métodos. Ficamos mais íntimos dos livros. Este esforço que você comentou será sempre necessário, pois apenas nós somos responsáveis pelo entendimento.
Ressalto que suas próximas dúvidas sempre serão bem-vindas, especialmente acompanhadas de curiosidades, idéias e tentativas.
Não tenho formação nem condições para lecionar cálculo, apenas gosto do assunto.
Desejo sucesso!
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda sobre Limites seno e exponencial
por gn66 » Sex Jun 03, 2011 12:02
- 8 Respostas
- 4692 Exibições
- Última mensagem por gn66

Sex Jun 03, 2011 16:34
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Ajuda nessa questão sobre limite
por IlgssonBraga » Sáb Jan 25, 2014 15:53
- 1 Respostas
- 3067 Exibições
- Última mensagem por Russman

Sáb Jan 25, 2014 17:51
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2556 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 4758 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- Sobre Limites
por thiagosaadoficial » Seg Fev 29, 2016 17:08
- 0 Respostas
- 1433 Exibições
- Última mensagem por thiagosaadoficial

Seg Fev 29, 2016 17:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ______________________
______________________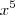 + 6x³ +9
+ 6x³ +9

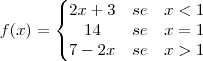
 , os
, os 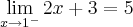

 , tanto é que
, tanto é que  .
.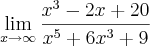
 , temos:
, temos: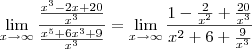


 .
. é a assíntota vertical que nunca e tocada pela hipérbole.
é a assíntota vertical que nunca e tocada pela hipérbole. é a assíntota horizontal que também nunca é tocada pela hipérbole.
é a assíntota horizontal que também nunca é tocada pela hipérbole.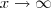 .
.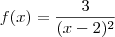
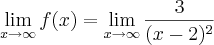

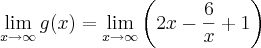
 , o que indica não existir assíntota horizontal (pense no gráfico).
, o que indica não existir assíntota horizontal (pense no gráfico).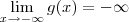 .
.

 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
