No papel quadriculado da figura a seguir http://diadematematica.com/vestibular/T ... /E1392.BMP, adota-se como unidade de comprimento o lado do quadrado hachurado. DE é paralelo a BC. Para que a área do triângulo ADE seja a metade da área do triângulo ABC, a medida de AD, na unidade adotada, é:
Bom, as áreas de figuras semelhantes são proporcionais, correto? A razão da semelhança das áreas é proporcional a razão de semelhança de lados correspondentes, também confere? Relacionei a área do triângulo maior a do menor(k²=24/12 k=
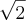 ) e os lados AB(que no meu livro,diferente do desenho que postei,tem 8 quadrados) ao lado AD(k=8/x). Relacionando as razões em proporção
) e os lados AB(que no meu livro,diferente do desenho que postei,tem 8 quadrados) ao lado AD(k=8/x). Relacionando as razões em proporção 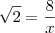 =
= 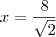 . É isso?
. É isso?

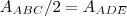
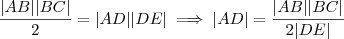
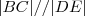 então ,
então , 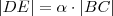 e também ,
e também ,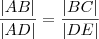 .Lembrando que ,
.Lembrando que ,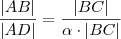
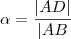 .Assim concluimos ,
.Assim concluimos ,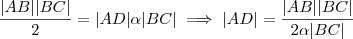
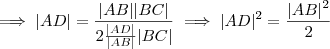 .Como |AB| > 0 implica ,
.Como |AB| > 0 implica ,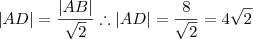 .
.
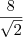 a
a 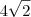 ? Por qual número simplificou? Perdoe a ignorância.
? Por qual número simplificou? Perdoe a ignorância.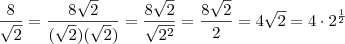
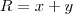 (onde x e y são números reais fixos )
(onde x e y são números reais fixos )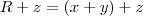 para todo z real .(
para todo z real .(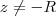 )
)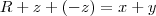
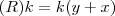 para todo k diferente de zero .
para todo k diferente de zero .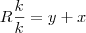 note que para todo k/k -{0} = 1 .
note que para todo k/k -{0} = 1 . ,se quisermos aproximar a expressão
,se quisermos aproximar a expressão 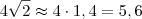 veja que é mais fácil fazer isso ,caso contrario :
veja que é mais fácil fazer isso ,caso contrario :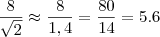


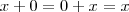


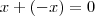

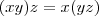
 ,
,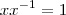 .
.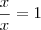 . Como 1 é o elemento neutro da multiplicação, não altera a expressão. No caso em questão, temos
. Como 1 é o elemento neutro da multiplicação, não altera a expressão. No caso em questão, temos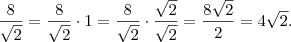

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
