Problema envolvendo geometria e area!

[bmachado]

O retângulo ABCD representa um terreno, e o trapézio sombreado, uma
construção a ser feita nele. Por exigências legais, essa construção deve ter uma área, no mínimo,
igual a 45% e, no máximo, igual a 60% do terreno. Determine os possíveis valores de x
Obs; N sei fazer imagem no site, segue link do retangulo:/www.colegioibituruna.com.br/2011/Downloads/Recuperacao/4_bimestre/Matematica%20-%203%20serie%20-%20EM.pdf

Obrigado, pois, ja achei dois resultados, porem, n o correto, que é (17,26)

[fraol]

Para colocar uma imagem no site, você pode fazer o seguinte:
Escolher "Adicionar um anexo" na parte debaixo da caixa de digitação da postagem, então escolher o arquivo, colocar um título para a imagem e clicar no botão "Adicionar um anexo". Depois disso, caso queira que a imagem apareça junto com a postagem você pode clicar no botão "Insira na linha" que fica junto da imagem na parte de baixo da sua digitação, como fiz aqui.

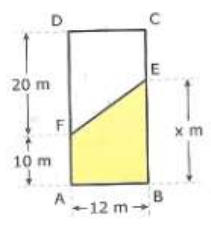
terreno

terreno.png (28.65 KiB) Exibido 3946 vezes

Quanto ao problema você pode resolvê-lo, respondendo as seguintes questões:

1) Qual é a área total do terreno?

2) Quanto é 45% dessa área total?

3) Quanto é 60% dessa área total?

4) Qual é a área da construção, no caso um trapézio de base maior m, base menor 10m e altura 12m?
(será uma função de primeiro grau em )

5) Agora você deve colocar que a função obtida em 4) deve ser maior que o resultado obtido em 2).

6) Também deve colocar que a função obtida em 4) deve ser menor que o resultado obtido em 3).

Ao desenvolver os passos acima você obterá exatamente a resposta do problema.

Quer tentar?

[bmachado]

Para colocar uma imagem no site, você pode fazer o seguinte:
Escolher "Adicionar um anexo" na parte debaixo da caixa de digitação da postagem, então escolher o arquivo, colocar um título para a imagem e clicar no botão "Adicionar um anexo". Depois disso, caso queira que a imagem apareça junto com a postagem você pode clicar no botão "Insira na linha" que fica junto da imagem na parte de baixo da sua digitação, como fiz aqui.

terreno.png

Quanto ao problema você pode resolvê-lo, respondendo as seguintes questões:

1) Qual é a área total do terreno?

2) Quanto é 45% dessa área total?

3) Quanto é 60% dessa área total?

4) Qual é a área da construção, no caso um trapézio de base maior m, base menor 10m e altura 12m?


Vou tentar de novo e retorno obrigado pelo passos
(será uma função de primeiro grau em )

5) Agora você deve colocar que a função obtida em 4) deve ser maior que o resultado obtido em 2).

6) Também deve colocar que a função obtida em 4) deve ser menor que o resultado obtido em 3).

Ao desenvolver os passos acima você obterá exatamente a resposta do problema.

Quer tentar?

[bmachado]

Para colocar uma imagem no site, você pode fazer o seguinte:
Escolher "Adicionar um anexo" na parte debaixo da caixa de digitação da postagem, então escolher o arquivo, colocar um título para a imagem e clicar no botão "Adicionar um anexo". Depois disso, caso queira que a imagem apareça junto com a postagem você pode clicar no botão "Insira na linha" que fica junto da imagem na parte de baixo da sua digitação, como fiz aqui.

terreno.png

Quanto ao problema você pode resolvê-lo, respondendo as seguintes questões:

1) Qual é a área total do terreno? 360

2) Quanto é 45% dessa área total? 162

3) Quanto é 60% dessa área total? 216

4) Qual é a área da construção, no caso um trapézio de base maior m, base menor 10m e altura 12m? (30x12)/2=180


Vou tentar de novo e retorno obrigado pelo passos
(será uma função de primeiro grau em )

5) Agora você deve colocar que a função obtida em 4) deve ser maior que o resultado obtido em 2).

6) Também deve colocar que a função obtida em 4) deve ser menor que o resultado obtido em 3).

Ao desenvolver os passos acima você obterá exatamente a resposta do problema.

Quer tentar?

[bmachado]

Para colocar uma imagem no site, você pode fazer o seguinte:
Escolher "Adicionar um anexo" na parte debaixo da caixa de digitação da postagem, então escolher o arquivo, colocar um título para a imagem e clicar no botão "Adicionar um anexo". Depois disso, caso queira que a imagem apareça junto com a postagem você pode clicar no botão "Insira na linha" que fica junto da imagem na parte de baixo da sua digitação, como fiz aqui.

terreno.png

Quanto ao problema você pode resolvê-lo, respondendo as seguintes questões:

1) Qual é a área total do terreno? 360

2) Quanto é 45% dessa área total? 162

3) Quanto é 60% dessa área total? 216

4) Qual é a área da construção, no caso um trapézio de base maior m, base menor 10m e altura 12m? (30x12)/2=180


Vou tentar de novo e retorno obrigado pelo passos
(será uma função de primeiro grau em )

5) Agora você deve colocar que a função obtida em 4) deve ser maior que o resultado obtido em 2).

6) Também deve colocar que a função obtida em 4) deve ser menor que o resultado obtido em 3).

Ao desenvolver os passos acima você obterá exatamente a resposta do problema.

Quer tentar?

Obrigado pelo processo pedagogico, consegui resolver, faleu, pois, eu estava já puto pq n conseguia!Abraco!