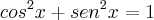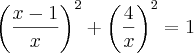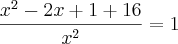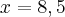por Lucio » Seg Dez 26, 2011 11:46
por Lucio » Seg Dez 26, 2011 11:46
Bom dia.
Me deparei com esse problema e não cheguei a resposta.
Eis o problema:
A altura de uma parede é de 4 m. Uma escada está apoiada na parede de modo que seu ponto mais alto coincide com a extremidade superior da parede e os pés da escada estão afastados da base da parede. Se os pés da escada forem afastados mais 1 m da parede, a escada cairá no chão, ficando com a parte superior rente à base da parede. Nessa situação, conclui-se que o comprimento da escada é igual a?
Resposta: 8,5m.
Tentativas:
Pelo Teorema de Pitágoras não consegui. (Parece que falta dados)
Por tangente não consegui. (Não tem os ângulos)
Prezados, desde já agradeço a ajuda de vcs professores.
Lúcio
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por fraol » Seg Dez 26, 2011 17:30
por fraol » Seg Dez 26, 2011 17:30
Oi Lúcio,
Deixa eu me intrometer nessa questão.
Você tem um triângulo no qual pode-se obter a relação do seno do ângulo oposto à parede assim:
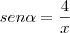
onde

é o comprimento da parede.
Também, pelo enunciado, sabemos que o
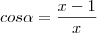
.
Agora basta aplicar a relação fundamental da trigonometria que o resultado vem.
Abç,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Lucio » Seg Dez 26, 2011 22:28
por Lucio » Seg Dez 26, 2011 22:28
Oi Francisco muito obrigado pela ajuda, confesso que passei um bom tempo tentando resolver do meu jeito e não consegui, mas agora cheguei ao resultado.
Vamos lá:
Relação fundamental da trigonometria
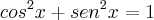
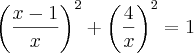
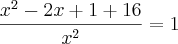


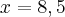
Francisco mais uma vez a sua ajuda foi fundamental para eu chegar ao resultado
Muito obrigado Lúcio.
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8725 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4713 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4825 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2541 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
-
- geometria plana
 por Abner » Seg Jan 31, 2011 17:53
por Abner » Seg Jan 31, 2011 17:53
- 3 Respostas
- 3681 Exibições
- Última mensagem por Abner

Ter Fev 01, 2011 17:31
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


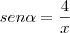 onde
onde  é o comprimento da parede.
é o comprimento da parede.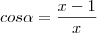 .
.