Olá,
um colega meu está estudando p/ concursos e sempre me proponho a ajudar com a parte de exatas. Certo dia, resolvi lhe fazer uma pergunta, com o objetivo de aguçar seu uso da intuição no estudo da matemática. Escrevi em um papel "x²", e lhe perguntei o que era. Após ele dar algumas respostas corretas (e deixei isso claro), respondi-lhe que aquilo era um quadrado. Ao que ele começou a discutir dizendo que eu estava errado, porem sem utilizar argumentação alguma, apenas dizendo que aquilo era uma potencia, um "x elevado ao quadrado", mas que não era um quadrado.
Pois bem, reconheço que, a rigor, não podemos dizer que "x²" é um quadrado, a menos que x pertança ao conjunto dos inteiros, porém não pode-se afirmar que não o seja, uma vez que o domínio não foi definido.
Gostaria de uma opinião de profissionais da área, como lidar com uma situação como essa. Apesar de não ser um profissional da área de matemática, gosto bastante, sempre me proponho a ajudar, e acho que esse tipo de intuição é muito importante na resolução de problemas novos, ou complexos à primeira vista.
Grato, desde já, pela atenção, e desculpas antecipadas caso tenha infrigido alguma regra.



 é um quadrado pois, geralmente, nos referimos como domínio da função o conjunto dos Naturais, então, sempre teremos um quadrado perfeito, mas se o domínio for outro, tipo os Reais, aí a coisa realmente muda de figura, por isso evito chamar essa função de quadrado...
é um quadrado pois, geralmente, nos referimos como domínio da função o conjunto dos Naturais, então, sempre teremos um quadrado perfeito, mas se o domínio for outro, tipo os Reais, aí a coisa realmente muda de figura, por isso evito chamar essa função de quadrado... representa uma parábola. Já a equação
representa uma parábola. Já a equação 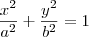 representa uma elipse. E há muitos outros exemplos.
representa uma elipse. E há muitos outros exemplos.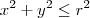 representa um círculo de raio r. Por outro lado,
representa um círculo de raio r. Por outro lado, 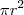 é a área desse círculo. Seria errado afirmar que
é a área desse círculo. Seria errado afirmar que 
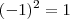 é a área do quadrado de lado -1. Mas, não faz sentido um lado com medida negativa. Portanto, uma pequena correção:
é a área do quadrado de lado -1. Mas, não faz sentido um lado com medida negativa. Portanto, uma pequena correção:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.