 por claudia » Qui Ago 14, 2008 18:35
por claudia » Qui Ago 14, 2008 18:35
Como faço para colocar uma figura ( uma circunferência) aqui?
-
claudia
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Ago 13, 2008 17:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pré-vestibular
- Andamento: formado
 por admin » Qui Ago 14, 2008 18:48
por admin » Qui Ago 14, 2008 18:48
Olá.

O site não gera as figuras, mas recomendo utilizar estes dois programas comentados aqui para construções geométricas e gráficos, no link também há dois exemplos, dentre outros pelo fórum:
viewtopic.php?f=118&t=289&p=741#p741Com a figura salva em seu computador, na tela de postagem de novo tópico, adicione como anexo e a imagem aparecerá.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por claudia » Sex Ago 15, 2008 16:38
por claudia » Sex Ago 15, 2008 16:38
Fábio, não consegui colocar a figura aqui, então a enviei por e-mail. Teria como dar uma olhada e me dar umas dicas?
Obrigada, Claudia
-
claudia
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Ago 13, 2008 17:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pré-vestibular
- Andamento: formado
 por admin » Sex Ago 15, 2008 17:01
por admin » Sex Ago 15, 2008 17:01
Olá Cláudia.
Para anexar a figura:
Selecione o arquivo salvo em seu computador:
Clique no botão "Adicionar um arquivo".
Após, você pode utilizar o botão "Prever" para confirmar como ficará sua mensagem.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por claudia » Sex Ago 15, 2008 17:18
por claudia » Sex Ago 15, 2008 17:18
Dados sobre a circunferência: Sendo O o centro da circunferência de raio unitário, então x=BC vale?
- Anexos
-
[O anexo não pode ser exibido, pois a extensão doc foi desativada pelo administrador.]
-
claudia
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Ago 13, 2008 17:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pré-vestibular
- Andamento: formado
 por admin » Sex Ago 15, 2008 17:26
por admin » Sex Ago 15, 2008 17:26
Cláudia, como é um outro problema, vou dividir o tópico, criando um novo.
Anexei novo arquivo como "imagem", sendo assim, ela aparece diretamente:
claudia escreveu:Dados sobre a circunferência: Sendo O o centro da circunferência de raio unitário, então x=BC vale?
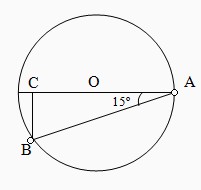
- circunferencia2.jpg (6.36 KiB) Exibido 14892 vezes
Sempre comente previamente suas tentativas de resolução.
Você também quis desenhar que o ângulo
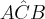
é reto?
Vamos conversando...
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por claudia » Sex Ago 15, 2008 18:18
por claudia » Sex Ago 15, 2008 18:18
Sim, e o arco AB = 150 e entre B e C= 30º
-
claudia
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Ago 13, 2008 17:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pré-vestibular
- Andamento: formado
 por admin » Sex Ago 15, 2008 18:33
por admin » Sex Ago 15, 2008 18:33
Cláudia, tente enviar uma figura
completa com os dados informados.
E o que quer dizer com?
claudia escreveu:e entre B e C= 30º
Após completar a figura sem deixar dúvidas de interpretação, teremos então apenas o enunciado do problema. Em seguida, comente suas tentativas para que eu possa ajudá-la, ok? Lembre-se das regras do fórum. Tentar
especificar a dúvida é importante.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por claudia » Sex Ago 15, 2008 20:31
por claudia » Sex Ago 15, 2008 20:31
Já enviei todos os dados que o problema deu. Os valores dos arcos fui eu que coloquei. O de 30º é o arco oposto ao ângulo de 15º. Não sei nem por onde começar.
-
claudia
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Ago 13, 2008 17:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pré-vestibular
- Andamento: formado
 por claudia » Sex Ago 15, 2008 20:34
por claudia » Sex Ago 15, 2008 20:34
Estas questões que estou enviando são algumas das 300 questões resolvidas por mim, de uma apostila, e que não consegui resolver. Suas dicas estão me ajudando bastante.
-
claudia
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Ago 13, 2008 17:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pré-vestibular
- Andamento: formado
 por admin » Sex Ago 15, 2008 21:57
por admin » Sex Ago 15, 2008 21:57
Olá Cláudia, boa noite!

Dica:
Tente utilizar outro dado, o raio unitário.
Trace um raio, o segmento OB. Anote seu valor na figura.
Marque o ângulo

.
Pense no triângulo retângulo

.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por claudia » Seg Ago 18, 2008 18:24
por claudia » Seg Ago 18, 2008 18:24
CONSEGUI!!!
Você é d+. Valeu!
-
claudia
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Ago 13, 2008 17:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pré-vestibular
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8719 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4706 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4820 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2539 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
-
- geometria plana
 por Abner » Seg Jan 31, 2011 17:53
por Abner » Seg Jan 31, 2011 17:53
- 3 Respostas
- 3674 Exibições
- Última mensagem por Abner

Ter Fev 01, 2011 17:31
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








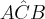 é reto?
é reto?




 Dica:
Dica: .
. .
.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.