-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480068 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 538314 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 502125 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 723955 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2158467 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por ezidia51 » Dom Nov 10, 2019 23:08
por ezidia51 » Dom Nov 10, 2019 23:08
Alguém pode me ajudar com este cálculo.Naõ estou consehuindo entender:
1)Suponha que, no triângulo ABC, tenhamos |AB| = 2|BC|. Além disso, suponha que o comprimento do lado [AC] seja um número inteiro. Então é possível afirmar que temos, necessariamente:
bc>3 bc>? bc>1 bc>2 bc>½
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por adauto martins » Ter Nov 12, 2019 20:04
por adauto martins » Ter Nov 12, 2019 20:04
usar a "lei dos cossenos"
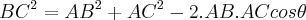

como
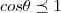
logo
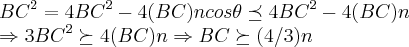
logo
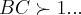
para o menor valor de n,n=1...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Ter Nov 12, 2019 22:08
por adauto martins » Ter Nov 12, 2019 22:08
uma correçao:
no desenvolvimento da questao,esqueci me do termo
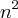
entao
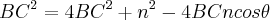
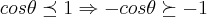

agora é resolver essa inequaçao,e usar o mesmo racionio posto anteriormente,n=1...termine-o
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo da area de um triangulo
por matway » Dom Set 04, 2011 20:36
- 2 Respostas
- 2704 Exibições
- Última mensagem por matway

Seg Set 05, 2011 09:04
Geometria Plana
-
- [Cálculo] Problema triângulo
por pires_ » Dom Dez 09, 2012 16:22
- 2 Respostas
- 2308 Exibições
- Última mensagem por pires_

Dom Dez 09, 2012 20:58
Cálculo: Limites, Derivadas e Integrais
-
- cálculo 1 area do triangulo
por ezidia51 » Qui Set 12, 2019 01:48
- 1 Respostas
- 3383 Exibições
- Última mensagem por adauto martins

Qua Out 02, 2019 16:54
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de perimetro do triangulo retangulo
por Marcinha » Dom Nov 13, 2011 16:12
- 1 Respostas
- 2615 Exibições
- Última mensagem por Andreza

Dom Nov 13, 2011 18:08
Geometria Plana
-
- Dúvida {Cálculo da área de um triângulo}
por Danilo » Qua Jul 11, 2012 05:40
- 2 Respostas
- 2530 Exibições
- Última mensagem por Danilo

Qua Jul 11, 2012 13:54
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


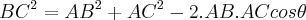

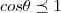
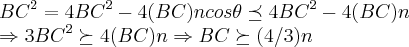
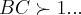
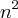 entao
entao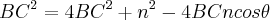
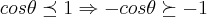



 , avisa que eu resolvo.
, avisa que eu resolvo.

