(escola militar do realengo-exame de admissao 1936)
divide-se o lado BC de um trapezio em dois segmentos BF e CF,proporcionais a 3 e 2 e,pelo ponto de divisao f,
traça-se uma reta EF paralela as bases.calcular EF sabendo que AB=38,5m e DC=12,45m.



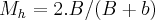 ,a qual nao precisaremos de usar aqui e sim o "teorema de tales,das paralelas" e semelhança de triangulos.vamos a soluçao:
,a qual nao precisaremos de usar aqui e sim o "teorema de tales,das paralelas" e semelhança de triangulos.vamos a soluçao: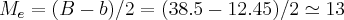 .bom agora temos parte do segmento EF,pedido pelo problema.
.bom agora temos parte do segmento EF,pedido pelo problema.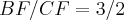 .bom usaremos agora semelhança dos triangulos BCD e BFP,onde p,é ponto de encontro da diagonal BD,com o segmento EF,ponto esse que é tambem limitante da "mediana de euler",que calculamos.logo,teremos:
.bom usaremos agora semelhança dos triangulos BCD e BFP,onde p,é ponto de encontro da diagonal BD,com o segmento EF,ponto esse que é tambem limitante da "mediana de euler",que calculamos.logo,teremos: ,que calculamos das semelhanças dos ditos triangulos,logo:
,que calculamos das semelhanças dos ditos triangulos,logo: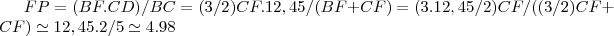
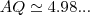


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.