-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478160 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531721 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495270 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 705434 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2121118 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Guga1981 » Qua Ago 29, 2018 18:51
por Guga1981 » Qua Ago 29, 2018 18:51
Boa tarde, senhores!
Estou lendo um artigo que trata dos três problemas clássicos gregos e, na parte que fala da máquina de Platão, me deparei com a suspeita de que a primeira relação
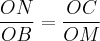
está equivocada:
Pela minha dedução o autor do artigo se enganou ao fazer a proporção dos triângulos MÔC e BÔN:
A relação correta não seria:
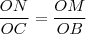
O que vocês acham?
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Gebe » Qua Ago 29, 2018 19:45
por Gebe » Qua Ago 29, 2018 19:45
A dedução do autor está correta.
Observe na sua figura a disposição dos angulos (que está certa).
A proporção é vista em relação aos angulos, portanto o segmento oposto ao angulo alpha, por exemplo, de um triangulo deve estar diretamente proporcional ao segmento oposto ao angulo alpha do outro triangulo.
A sua proporção ficou inversamente proporcional.
ex.: Segundo a proporção que você propõe, mantendo-se MOC sem alterações, se aumentarmos o comprimento ON, teriamos de diminuir OB para manter a proporção entre MOC e BON o que não aconteceria.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Guga1981 » Sáb Set 01, 2018 01:08
por Guga1981 » Sáb Set 01, 2018 01:08
Gebe escreveu:A dedução do autor está correta.
Observe na sua figura a disposição dos angulos (que está certa).
A proporção é vista em relação aos angulos, portanto o segmento oposto ao angulo alpha, por exemplo, de um triangulo deve estar diretamente proporcional ao segmento oposto ao angulo alpha do outro triangulo.
A sua proporção ficou inversamente proporcional.
ex.: Segundo a proporção que você propõe, mantendo-se MOC sem alterações, se aumentarmos o comprimento ON, teriamos de diminuir OB para manter a proporção entre MOC e BON o que não aconteceria.
Mas, olha, no primeiro triangulo (o OMC) o segmento oposto ao angulo alpha é o segmento OM enquanto que no segundo triangulo (o BON) o segmento oposto ao ângulo alpha é o OB. Não é um lado de um triângulo no numerador da fração e o outro lado correspondente no denominador? Se for isso, a fração fica:
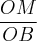
e não
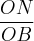
.
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Gebe » Sáb Set 01, 2018 15:25
por Gebe » Sáb Set 01, 2018 15:25
Não é um lado de um triângulo no numerador da fração e o outro lado correspondente no denominador
Na verdade isso é mais uma dica/macete de como escrever a relação.
Podemos escrever de varias formas essa proporcionalidade:
-> ON/OB = OC/OM
-> ON/OC = OB/OM
-> OM/OB = OC/ON -> forma
derivada da tua duvida
-> ON.OM = OC.OB
-> (ON.OM) / (OC.OB) = 1
-> 1/(ON.OM) = 1/(OC.OB)
E varias outras formas, tendo apenas que respeitar a proporcionalidade.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Guga1981 » Sáb Set 01, 2018 22:18
por Guga1981 » Sáb Set 01, 2018 22:18
Ah... eu não sabia que dava para relacionar a razão dos dois lados de um mesmo triângulo pelos dois lados de outro triângulo! Eu só havia aprendido a fazer a proporção de um lado do primeiro triângulo pelo lado correspondente do segundo triângulo igual a outro lado do primeiro sobre outro lado do segundo. Obrigado! Aprendi mais uma!
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Gebe » Sáb Set 01, 2018 22:27
por Gebe » Sáb Set 01, 2018 22:27
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Será que o meu raciocínio esta correto!?
por Evaldo » Qua Dez 30, 2009 12:12
- 1 Respostas
- 4879 Exibições
- Última mensagem por Neperiano

Sex Set 23, 2011 19:33
Estatística
-
- LOGARITIMO - SERA QUE ESTA CERTO ?
por lais1906 » Sáb Out 13, 2012 01:44
- 7 Respostas
- 8098 Exibições
- Última mensagem por MarceloFantini

Sáb Out 13, 2012 17:54
Logaritmos
-
- Será que está correta a resolução e o resultado
por Douglas16 » Dom Mar 10, 2013 16:55
- 3 Respostas
- 4106 Exibições
- Última mensagem por Douglas16

Dom Mar 10, 2013 23:37
Cálculo: Limites, Derivadas e Integrais
-
- [Matriz quadrada] Será que o gabarito está errado?
 por Guga1981 » Qua Out 11, 2017 11:26
por Guga1981 » Qua Out 11, 2017 11:26
- 2 Respostas
- 10388 Exibições
- Última mensagem por Guga1981

Ter Out 17, 2017 19:00
Matrizes e Determinantes
-
- ajuda, deu errada a resposta
por Guilhermme » Qua Mar 28, 2012 13:31
- 2 Respostas
- 3524 Exibições
- Última mensagem por ednaldo1982

Qua Mar 28, 2012 16:41
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 16 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
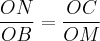 está equivocada:
está equivocada: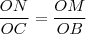



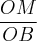 e não
e não 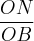 .
.