-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478483 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533137 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496650 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 709537 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2128189 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Matheus Macedo » Ter Ago 29, 2017 20:31
por Matheus Macedo » Ter Ago 29, 2017 20:31
No piso de um salão retangular foram usados 1200 tacos quadrados. Em outro salão retangular, cuja as dimensões são 2 vezes maiores que as dimensões do primeiro, quantos desses tacos devem ser usados?
-
Matheus Macedo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Ago 29, 2017 20:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qua Ago 30, 2017 00:51
por DanielFerreira » Qua Ago 30, 2017 00:51
Matheus Macedo escreveu:No piso de um salão retangular foram usados 1200 tacos quadrados. Em outro salão retangular, cuja as dimensões são 2 vezes maiores que as dimensões do primeiro, quantos desses tacos devem ser usados?
Olá Matheus, seja bem-vindo!
Sejam

a quantidade de tacos na horizontal do piso e
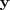
a quantidade de tacos na vertical do piso. Então, pelo princípio multiplicativo, temos que:
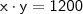
Por conseguinte, consideramos outro salão cujas dimensões são:

e
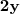
. Com efeito,
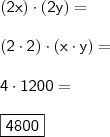
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Matheus Macedo » Qua Ago 30, 2017 18:30
por Matheus Macedo » Qua Ago 30, 2017 18:30
DanielFerreira escreveu:Matheus Macedo escreveu:No piso de um salão retangular foram usados 1200 tacos quadrados. Em outro salão retangular, cuja as dimensões são 2 vezes maiores que as dimensões do primeiro, quantos desses tacos devem ser usados?
Olá Matheus, seja bem-vindo!
Sejam

a quantidade de tacos na horizontal do piso e
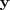
a quantidade de tacos na vertical do piso. Então, pelo princípio multiplicativo, temos que:
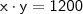
Por conseguinte, consideramos outro salão cujas dimensões são:

e
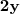
. Com efeito,
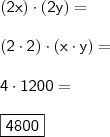
Obrigado pelas boas-vindas!!
E muito obrigado por me ajudar com essa questão; eu estava na dúvida se multiplicava 2x e 2y ou se apenas pegava os 1200 e multiplicava por 2.
Mais uma vez, obrigado.
-
Matheus Macedo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Ago 29, 2017 20:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sex Set 01, 2017 22:05
por DanielFerreira » Sex Set 01, 2017 22:05
Não há e quê!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana Comprimento da dobra em um Retângulo
por Lana Brasil » Sex Out 17, 2014 10:34
- 1 Respostas
- 1600 Exibições
- Última mensagem por adauto martins

Sáb Out 18, 2014 14:29
Geometria Plana
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8168 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4104 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4376 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2153 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 16 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 a quantidade de tacos na horizontal do piso e
a quantidade de tacos na horizontal do piso e 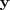 a quantidade de tacos na vertical do piso. Então, pelo princípio multiplicativo, temos que:
a quantidade de tacos na vertical do piso. Então, pelo princípio multiplicativo, temos que: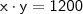
 e
e 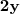 . Com efeito,
. Com efeito,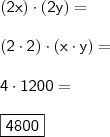

a quantidade de tacos na horizontal do piso e
a quantidade de tacos na vertical do piso. Então, pelo princípio multiplicativo, temos que:
e
. Com efeito,




 , avisa que eu resolvo.
, avisa que eu resolvo.

