-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478709 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534818 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498414 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 714310 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2136710 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por matheussodre » Qua Fev 22, 2017 22:44
por matheussodre » Qua Fev 22, 2017 22:44
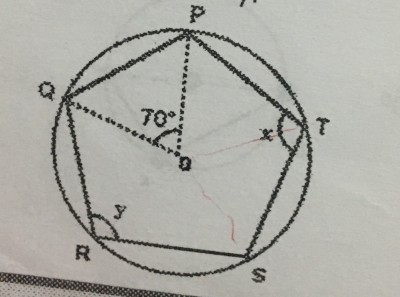
(FCC) Seja o pentágono PQRST da figura, inscrito na circunferência de centro O. Sabe-se que POQ mede 70º. Chamando de x e y os ângulos PTS e QRS, respectivamente, determine x+y:
Não sei nem pode onde começar.
Quero uma ideia pra tentar resolver
- Anexos
-
-
matheussodre
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 22, 2017 22:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por 314159265 » Qui Fev 23, 2017 06:34
por 314159265 » Qui Fev 23, 2017 06:34
Matheus,
Basta saber de uma propriedade: quando você tem um ângulo inscrito em uma circunferência, ele vale metade do arco.
Ou seja, o ângulo x vai ser metade do arco PQRS e o ângulo y vai ser metade do arco STPQ. Se você somar esses dois arcos, vai encontrar que eles são 360º + 70º. Se x + y é a metade disso, então a resposta é (360+70)/2 = 215.
Está correta?
-
314159265
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Fev 13, 2017 02:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por matheussodre » Qui Fev 23, 2017 14:49
por matheussodre » Qui Fev 23, 2017 14:49
Está sim. Muito obrigado! Mas por que a soma dos arcos dá 360°+70°?
-
matheussodre
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 22, 2017 22:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por 314159265 » Qui Fev 23, 2017 15:13
por 314159265 » Qui Fev 23, 2017 15:13
Some os dois arcos de x e y. Vai dar uma circunferência inteira e vão sobrar 70º ainda.
-
314159265
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Fev 13, 2017 02:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por matheussodre » Sex Fev 24, 2017 13:53
por matheussodre » Sex Fev 24, 2017 13:53
Faz sentido! Obrigado de novo
-
matheussodre
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 22, 2017 22:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por JayJay01 » Seg Abr 24, 2017 01:18
por JayJay01 » Seg Abr 24, 2017 01:18
A informação é boa, graças
-
JayJay01
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Abr 24, 2017 01:14
- Formação Escolar: SUPLETIVO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Triângulo Isósceles inscrito na circunferência]
 por Gustavo Gomes » Dom Out 14, 2012 23:22
por Gustavo Gomes » Dom Out 14, 2012 23:22
- 2 Respostas
- 11774 Exibições
- Última mensagem por Gustavo Gomes

Seg Out 15, 2012 23:27
Geometria Plana
-
- Explicação sobre triângulo inscrito em circunferência
por tom_junior » Ter Jun 30, 2009 23:31
- 1 Respostas
- 4904 Exibições
- Última mensagem por Marcampucio

Qua Jul 01, 2009 14:47
Geometria Plana
-
- [Triângulo inscrito na circunferência inscrita no quadrado]
 por Mayra Luna » Qui Out 18, 2012 19:05
por Mayra Luna » Qui Out 18, 2012 19:05
- 4 Respostas
- 2795 Exibições
- Última mensagem por Mayra Luna

Qui Out 18, 2012 21:42
Trigonometria
-
- Determinar o lado do pentágono
por leandrynhucarioca » Seg Ago 15, 2011 23:58
- 1 Respostas
- 1488 Exibições
- Última mensagem por Molina

Ter Ago 16, 2011 15:04
Geometria Plana
-
- Demonstração da razão aurea no pentagono.
por benni » Dom Out 16, 2011 15:13
- 2 Respostas
- 2135 Exibições
- Última mensagem por benni

Sáb Out 22, 2011 13:14
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 16 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.










 , avisa que eu resolvo.
, avisa que eu resolvo.

