 por fefehawaii » Qui Out 21, 2010 13:51
por fefehawaii » Qui Out 21, 2010 13:51
Um retângulo IFRJ intersecta uma circunferência nos pontos A, B, C e D como mostrado na figura a seguir.sabendo-se que IA = 6, AB = 10 e JC = 4, assinale, dentre os valores abaixo, a medida do segmento CD.
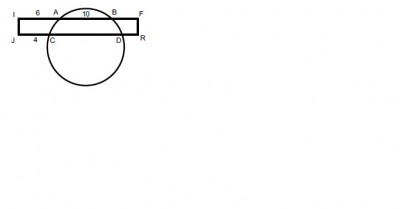
- tentei utilizar semelhanca de triangulos para achar o lado do retangulo, mas os resultados foram redundantes, recaindo nas mesmas definicoes, depoi utilizei potencia de ponto utilizando o mesmo tracado que fiz para obter triangulos e usar semelhanca, mas nao obtive exito, por nao passar pelo centro da circunferencia acabaram meus truques e nao consegui resolver o problema, peco ajuda...
(A) 14
(B) 15
(C) 16
(D) 17
(E) 18
resp (D)
-
fefehawaii
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Out 20, 2010 22:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia mecanica
- Andamento: cursando
 por VtinxD » Sáb Out 23, 2010 03:39
por VtinxD » Sáb Out 23, 2010 03:39
Fazendo a projeção ortogonal C na segmento IF,temos C', que possui IC'=JC então a distancia de C'A=AI-CJ=6-4=2 .Perceba que o polígono formado por ABCD é um trapézio e melhor ainda , isósceles pois os arcos AC e BD são iguais.Agora fazendo a projeção ortogonal de A em JR ,temos A',que possui AC'=CA' .Como propriedade do trapézio isósceles temos B'D=A'C,B' é a projeção ortogonal em JR, e como CD=B'D +A'C+A'B'==>CD=2+2+10=14
Se o gabarito estiver correto então também estou com duvida nessa questão,pois para mim a resolução parece correta.
Desculpe por não fazer a figura mas não sei faze-la.Espero que tenha entendido.Boa noite
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Retângulo/Circunferência
por DanielFerreira » Qui Mar 03, 2011 11:40
- 1 Respostas
- 1857 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 14:31
Geometria Plana
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4041 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- [circunferência] Questão de reta secante a circunferência
por danielleecb » Qui Jun 07, 2012 23:26
- 1 Respostas
- 1879 Exibições
- Última mensagem por MarceloFantini

Sex Jun 08, 2012 12:24
Geometria Analítica
-
- Retângulo
por Roberta » Qui Jun 19, 2008 18:07
- 8 Respostas
- 9997 Exibições
- Última mensagem por MarceloFantini

Ter Jan 05, 2010 23:37
Geometria Plana
-
- Retângulo
por Pri Ferreira » Qua Mar 21, 2012 14:03
- 1 Respostas
- 1288 Exibições
- Última mensagem por LuizAquino

Sex Mar 23, 2012 11:05
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
.



