por Balanar » Dom Set 26, 2010 12:00
por Balanar » Dom Set 26, 2010 12:00
No triângulo retângulo ABC da figura seguinte,
M é o ponto médio de
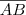
é o segmento

é paralelo ao lado
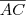
.
Sendo BC=6 , calcule a medida do segmento


Resolução:
Sendo M o ponto médio de 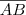 e
e  paralelo ao lado
paralelo ao lado 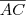 , então N é ponto médio de
, então N é ponto médio de  .
.Assim, os segmentos
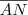
e

são medianas e P é o baricentro do triângulo ABC.
Logo :
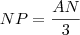
Mas
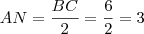
Portanto
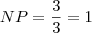
Resposta:
NP=1
Eu não entendi a seguinte parte:
Sendo M o ponto médio de 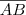 e
e  paralelo ao lado
paralelo ao lado 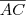 então N é ponto médio de
então N é ponto médio de  .Logo :
.Logo :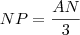
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Dom Set 26, 2010 12:24
por Elcioschin » Dom Set 26, 2010 12:24
Os triângulos ABC e MBN são semelhantes (tem os mesmos ângulos internos)
Se M é o ponto médio de AB ------> N é o ponto médio de BC
Neste caso teremos ----> AM = MB e BN = NC
Logo AN e CM são medianas.
As medianas sempre se dividem em segmentos na relação 1:2 ----> NP = AN/3
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Balanar » Dom Set 26, 2010 13:46
por Balanar » Dom Set 26, 2010 13:46

Eu provaria que que N é ponto médio de

assim:

pelo caso
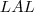
Assim temos que:


E isso certo?
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Dom Set 26, 2010 14:04
por Elcioschin » Dom Set 26, 2010 14:04
Esqueça o ponto X e faça a semelhança como eu indiquei:
AM = MB -----> AB = 2MB = 2AM
AB/BC = MB/NB
2*MB/BC = MB/NB
BC = 2*NB ----> N é o ponto médio de BC
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Balanar » Dom Set 26, 2010 14:12
por Balanar » Dom Set 26, 2010 14:12
Nossa, vlw.

-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Balanar » Dom Set 26, 2010 14:42
por Balanar » Dom Set 26, 2010 14:42
Como ele sabe que aquele e o ponto P é baricentro não teria que ter uma mediana passando por P ?
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Seg Set 27, 2010 09:20
por Elcioschin » Seg Set 27, 2010 09:20
Não entendí sua pergunta.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Balanar » Seg Set 27, 2010 15:00
por Balanar » Seg Set 27, 2010 15:00
Minha dúvida era a seguinte se duas medianas passam pelo mesmo ponto a terceira automaticamente passa pelo terceiro ponto formando assim o baricentro, certo?
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Coordenadas do Baricentro
por Cleyson007 » Sáb Fev 13, 2010 14:22
- 1 Respostas
- 4512 Exibições
- Última mensagem por MarceloFantini

Dom Fev 14, 2010 00:44
Geometria Analítica
-
- Baricentro e Elipse
por Aparecida » Dom Fev 12, 2012 19:58
- 1 Respostas
- 4520 Exibições
- Última mensagem por soraya santiago

Qui Fev 16, 2012 11:32
Geometria Plana
-
- Baricentro geometria analítica importante
 por elisamaria » Sex Jun 12, 2015 18:26
por elisamaria » Sex Jun 12, 2015 18:26
- 0 Respostas
- 1966 Exibições
- Última mensagem por elisamaria

Sex Jun 12, 2015 18:26
Geometria Analítica
-
- [Cálculo de Baricentro] com um vértice e um ponto médio
por Matheus Lacombe O » Dom Mai 27, 2012 18:49
- 1 Respostas
- 1928 Exibições
- Última mensagem por DanielFerreira

Dom Mai 27, 2012 21:24
Geometria Analítica
-
- [Geometria Plana - Triângulo Isósceles] Baricentro
por raimundoocjr » Seg Jan 28, 2013 15:31
- 5 Respostas
- 4659 Exibições
- Última mensagem por raimundoocjr

Seg Jan 28, 2013 19:38
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
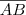 é o segmento
é o segmento  é paralelo ao lado
é paralelo ao lado 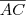 .
.

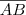 e
e  paralelo ao lado
paralelo ao lado 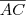 , então N é ponto médio de
, então N é ponto médio de  .
.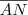 e
e  são medianas e P é o baricentro do triângulo ABC.
são medianas e P é o baricentro do triângulo ABC.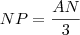
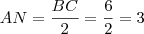
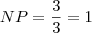
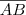 e
e  paralelo ao lado
paralelo ao lado 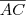 então N é ponto médio de
então N é ponto médio de  .
.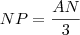




 pelo caso
pelo caso