Inscreveremos(não estranhe! É assim que se escreve, mesmo

) o decágono em uma circunferência de raio

e o dividiremos em
dez triângulos
congruentes, conforme abaixo:
Como todos os dez triângulos são congruentes, o ângulo central mede
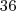
º e, como o triângulo é isóceles, os outros dois ângulos medem
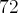
º.
Tracemos a bissetriz relativa a um dos ângulos de
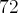
º , dividindo-o portanto em dois ângulos de
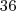
º . Obteremos, assim, dois novos triângulos isóceles que são semelhantes, pelo critério
ângulo-ângulo.
Na figura acima, os ângulos em verde medem
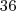
º e em vermelho medem
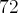
º . Pelos triângulos isóceles, os lados demarcados são congruentes e medem
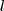
, isto é, o lado do decágono.
Da semelhança dos triângulos supracitados, temos que:
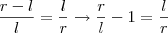
, se chamarmos
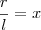
, então:
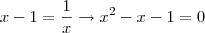
Resolvendo a equação do segundo grau em

, obtemos duas raízes, uma delas negativa. Nos interessa somente a raiz positiva, a saber:
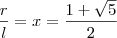
e, portanto,
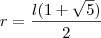
Voltemos ao triângulo principal de lados
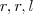
. Aplicando o Teorema dos Cossenos, temos que:
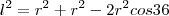
º , isto é,
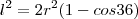
e fazendo uso da relação entre

e
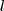
, temos:
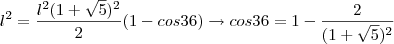
e, portanto,
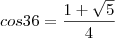
Ora, do Teorema Fundamental da Trigonometria, temos que:
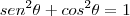
; assim
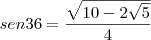
Ainda no triângulo principal, pela Lei das Áreas, temos que a área do triângulo pode ser dada por:
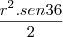
e, fazendo uso da relação já calculada entre

e
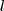
, bem como, do valor de
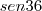
º, temos que:
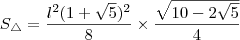
Seja

a área do decágono, então
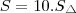
. Assim:
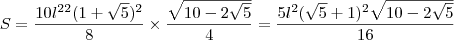
, que é a área do decágono regular em função do comprimento do seu lado.
Não consegui entender o suposto gabarito, mas desde já digo que não existem erros nessa resolução.

Depois você revê.


 e o dividiremos em
e o dividiremos em 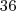 º e, como o triângulo é isóceles, os outros dois ângulos medem
º e, como o triângulo é isóceles, os outros dois ângulos medem 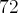 º.
º.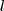 , isto é, o lado do decágono.
, isto é, o lado do decágono.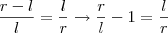 , se chamarmos
, se chamarmos 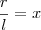 , então:
, então: 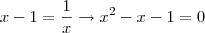
 , obtemos duas raízes, uma delas negativa. Nos interessa somente a raiz positiva, a saber:
, obtemos duas raízes, uma delas negativa. Nos interessa somente a raiz positiva, a saber: 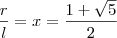 e, portanto,
e, portanto, 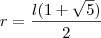
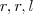 . Aplicando o Teorema dos Cossenos, temos que:
. Aplicando o Teorema dos Cossenos, temos que: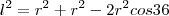 º , isto é,
º , isto é, 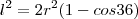 e fazendo uso da relação entre
e fazendo uso da relação entre 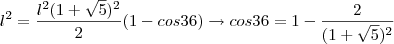 e, portanto,
e, portanto, 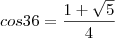
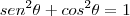 ; assim
; assim 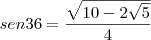
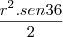 e, fazendo uso da relação já calculada entre
e, fazendo uso da relação já calculada entre 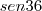 º, temos que:
º, temos que: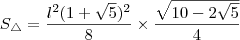
 a área do decágono, então
a área do decágono, então 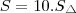 . Assim:
. Assim: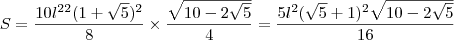 , que é a área do decágono regular em função do comprimento do seu lado.
, que é a área do decágono regular em função do comprimento do seu lado.

 .
.
 :
: