-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480816 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 543124 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 506846 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 737211 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2185038 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Guga1981 » Ter Mai 29, 2018 17:39
por Guga1981 » Ter Mai 29, 2018 17:39
Amigos, estou resolvendo provas anteriores da univesp e me deparei com a questão abaixo.
Não consigo estabelecer um critério para calcular a altura do triangulo inscrito para daí calcular a sua área.
Sei somente que a resposta certa é a letra D porque, se considerar a altura do triangulo como o diâmetro da circunferência, o valor da área será 130 cm², mas como a altura é um pouquinho menor do que o diâmetro eu assinalei a opção D (125 cm²). Mas como calcular essa resposta com exatidão?
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por DanielFerreira » Qui Mai 31, 2018 11:57
por DanielFerreira » Qui Mai 31, 2018 11:57
Olá
Guga!
Note que:
-
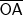
corresponde ao raio da circunferência, portanto, ele mede a metade do diâmetro;
-
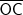
também é raio;
-
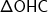
é retângulo em

;
Desse modo, podes determinar a medida do cateto
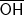
.
Qualquer dúvida, comente!!
Atentamente,
Daniel Ferreira.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Guga1981 » Sex Jun 01, 2018 21:33
por Guga1981 » Sex Jun 01, 2018 21:33
Muito bom!!!
Aí eu Calculo a altura de H até O fazendo:
13² = OH² + 5²
169 = oh² + 25
OH =
![\sqrt[2]{144} \sqrt[2]{144}](/latexrender/pictures/d86c95e7a1d45a5b6e7d0c89dd9a31b1.png)
OH = 12
E calculo a área do triângulo ABC como sendo

= 125 m²
Muito obrigado!
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Guga1981 » Sex Jun 01, 2018 21:35
por Guga1981 » Sex Jun 01, 2018 21:35
Vocês poderiam por favor indicar um bom fórum de física?
Estou precisando tirar dúvidas de física e estou tendo dificuldades.
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular perímetro do quadrado] através da área do triângulo
 por lukasmetal » Qua Nov 30, 2011 12:11
por lukasmetal » Qua Nov 30, 2011 12:11
- 3 Respostas
- 3473 Exibições
- Última mensagem por lukasmetal

Qui Dez 01, 2011 12:19
Geometria Plana
-
- Como calcular lado de um Triângulo Escaleno?
por Lothor » Dom Jul 31, 2011 02:37
- 1 Respostas
- 1875 Exibições
- Última mensagem por giulioaltoe

Dom Jul 31, 2011 14:53
Trigonometria
-
- Duvida como achar a area do triangulo
 por renataf » Qui Dez 09, 2010 19:48
por renataf » Qui Dez 09, 2010 19:48
- 5 Respostas
- 4190 Exibições
- Última mensagem por Jefferson

Sáb Dez 11, 2010 22:45
Geometria Analítica
-
- Triângulo inscrito
 por laisv11 » Qui Mai 28, 2009 16:33
por laisv11 » Qui Mai 28, 2009 16:33
- 4 Respostas
- 10243 Exibições
- Última mensagem por Molina

Sáb Mai 30, 2009 22:05
Geometria Plana
-
- Triângulo Inscrito
por Fogodc » Seg Abr 05, 2010 23:33
- 0 Respostas
- 1393 Exibições
- Última mensagem por Fogodc

Seg Abr 05, 2010 23:33
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


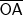 corresponde ao raio da circunferência, portanto, ele mede a metade do diâmetro;
corresponde ao raio da circunferência, portanto, ele mede a metade do diâmetro;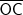 também é raio;
também é raio;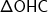 é retângulo em
é retângulo em  ;
;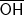 .
.
![\sqrt[2]{144} \sqrt[2]{144}](/latexrender/pictures/d86c95e7a1d45a5b6e7d0c89dd9a31b1.png)


 .
.



