[geometria plana] Unesp

[my2009]

Olá pessoal, boa noite.

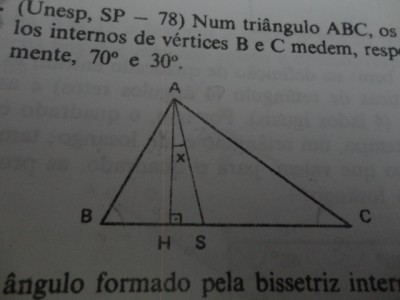
Num triângulo ABC, os ângulos internos de vértices B e C medem, respectivamente, 70º e 30º
O ângulo formado pela bissetriz interna AS e a altura AH mede:

a) 50º
b) 40º
c) 25º
d) 20º
e) 18º

Tentei fazer o seguinte :

A+B +C =180º

A = y+x+z = 80
como já tinha o ângulo B e o ângulo reto, achei y=20 alguém pode continuar?

[Gebe]

Ok, seguindo o teu desenvolvimento (que está certo):

A bissetriz separa o angulo  em duas partes iguais de 40º que são justamente os angulos (x+y) e z (seguindo tua nomenclatura).
Ja que é pedido o angulo "x", temos:

(x+y) = 40º

(x+20º) = 40º

x = 20º (Letra d)

[my2009]

Obrigada