[geometria plana] Cesgranrio

[my2009]

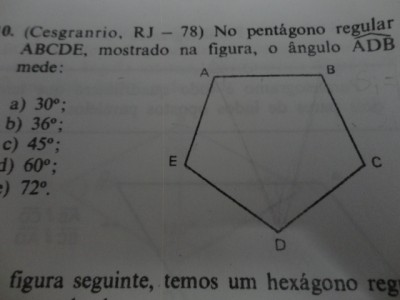
No pentágono regular ABCDE, mostrado na figura, o ângulo ADB mede :

a) 30º
b) 36º
c) 45º
d) 60º
e) 72º

Si =(n-2). 180º
Si= (5-2).180º
Si= 540º

[Gebe]

Há algumas formas de pensar neste problema. Vou colocar duas delas.
1ª: Seguindo a regularidade do poligono sabemos que todos angulos internos valem 108º (no total de 540º como tu colocou). Agora, porque o poligono é regular, podemos afirmar que EDA , ADB e BDC são iguais. Por fim então temos que se estes 3 angulos são iguais e somados valem 108º, ADB vale 36º.

Este foi jeito mais "preguiçoso". A outra forma seria mostrar que de fato EDA e BDC valem 36º e disto constatar que ADB tambem vale 36º.
Para isso fazemos o seguinte:
1) desenhamos uma linha unindo BD (ou AD), temos um triangulo BCD.
2) Agora desenhamos um segmento unindo C e o ponto medio de BD. Porque o pentagono é regular sabemos que este segmento dividirá o triangulo BCD em dois triangulos retangulos com o angulo MCD igual a 54º (108/2). ["M" é o ponto medio de BD]
3) Do triangulo retangulo MCD conhecemos 2 dos 3 angulos. Para calcular o que falta basta achar o suplemento (MDCº + 90º + 54º = 180º). MDCº = 36º = BDCº
4) Fazendo os mesmos passos achamos que EDA vale tambem 36º. Logo ADBº + 36º + 36º = 108º --> ADBº = 36º

Espero ter ajudado, bons estudos!

[my2009]

Olá Gebe, agradeço muito a explicação e a paciência. Obrigada !