Boa noite, Ana Paula.
Você conseguiu entender o que o problema diz? Fiz um desenho para visualizar melhor:
Ele quer dizer que os lados dessas duas figuras são iguais e que a digonal (
em vermelho) vale
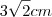
.
A fórmula da diagonal de um quadrado é dada por
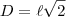
.
Então substituindo (em D) o valor da diagonal que é dado no enunciado, você vai descobrir
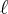
e esse é o valor do lado do quadrado, consequentemente o valor do lado do triângulo também.
Sabendo o lado do triângulo você precisa descobrir a área do mesmo. Utilize a fórmula
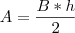
, onde B é a base do triângulo (ou seja, é
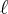
}; e h é a altura do triângulo, que é dado por
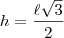
Tente aí e informe se tiver alguma dúvida.
Bom estudo,



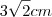 .
.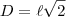 .
.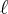 e esse é o valor do lado do quadrado, consequentemente o valor do lado do triângulo também.
e esse é o valor do lado do quadrado, consequentemente o valor do lado do triângulo também.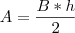 , onde B é a base do triângulo (ou seja, é
, onde B é a base do triângulo (ou seja, é 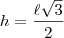



 , avisa que eu resolvo.
, avisa que eu resolvo.

