 por Lais-Lima » Sáb Set 13, 2014 13:08
por Lais-Lima » Sáb Set 13, 2014 13:08
Na figura seguinte, sabe-se que
AB = AD e que o
ângulo ABC menos o ângulo ACB é 30°. Então o
ângulo CBD é igual a:
Comecei o exercício tentando nomear os ângulos.
ABD =

ADB =

BAD =

CDB =

+

CBD =

BCD =

À partir daí estou tentando encontrar igualdades, mas não consigo resolver até o final. Por exemplo:
2

+

= 180°

+

+

+

= 180°

+

-

= 30°
Alguém pode me ajudar?
- Anexos
-
![20140913_102252-1[1].jpg (1.49 MiB) Exibido 1088 vezes 20140913_102252-1[1].jpg](./download/file.php?id=2086&t=1)
-
Lais-Lima
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Set 13, 2014 12:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pessoa Estranha » Dom Set 14, 2014 23:13
por Pessoa Estranha » Dom Set 14, 2014 23:13
Olá!
Note que:
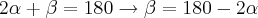
Substituindo na segunda igualdade:
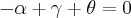
Daí, na terceira igualdade:
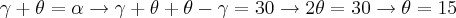
É este o resultado?
Entendeu?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Lais-Lima » Seg Set 15, 2014 17:37
por Lais-Lima » Seg Set 15, 2014 17:37
Isso! Entendi sim, obrigada!

-
Lais-Lima
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Set 13, 2014 12:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Triângulos] Pontos Notáveis
 por Lais-Lima » Seg Set 15, 2014 17:56
por Lais-Lima » Seg Set 15, 2014 17:56
- 0 Respostas
- 725 Exibições
- Última mensagem por Lais-Lima

Seg Set 15, 2014 17:56
Geometria Plana
-
- Pontos notáveis de um triÂngulo
 por Brufofs » Ter Mar 13, 2012 19:37
por Brufofs » Ter Mar 13, 2012 19:37
- 5 Respostas
- 5104 Exibições
- Última mensagem por Brufofs

Qua Mar 14, 2012 14:46
Geometria Plana
-
- pontos notáveis do triângulo
por lenda » Qua Jul 18, 2012 17:01
- 8 Respostas
- 6361 Exibições
- Última mensagem por lenda

Qui Jul 19, 2012 15:38
Geometria Plana
-
- pontos notáveis do triângulo
por lenda » Qua Jul 18, 2012 17:23
- 2 Respostas
- 2068 Exibições
- Última mensagem por lenda

Qua Jul 18, 2012 20:20
Geometria Plana
-
- pontos notáveis do triângulo
por lenda » Qua Jul 18, 2012 20:57
- 2 Respostas
- 1878 Exibições
- Última mensagem por lenda

Qui Jul 19, 2012 14:53
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 +
+ 


 +
+  = 180°
= 180° +
+  +
+  +
+  = 180°
= 180° +
+  -
-  = 30°
= 30°

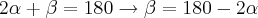
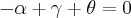
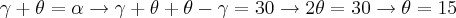

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.