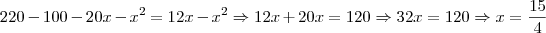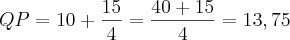por Micael » Qua Abr 17, 2013 22:29
por Micael » Qua Abr 17, 2013 22:29
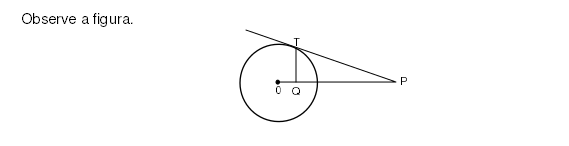
Observe a figura :
Nela o círculo tem o centro O e raio 6 e OP=16. A reta PT é tangente ao circulo em T eo segmento --TQ é perpendicular á reta OP assim sendo, o comprimento do segmento QP é? da uma ajuda nesse exercicio...
R:13,75
- Anexos
-
- geometria.png (6.1 KiB) Exibido 6748 vezes
Editado pela última vez por
Micael em Qui Abr 18, 2013 10:21, em um total de 2 vezes.
-
Micael
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Jan 31, 2013 00:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Qui Abr 18, 2013 08:10
por nakagumahissao » Qui Abr 18, 2013 08:10
Não tem algo errado nesta questão? OP = 16 e é perguntado quanto vale OP?
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Micael » Qui Abr 18, 2013 10:22
por Micael » Qui Abr 18, 2013 10:22
Pronto arrumei! .... alguem pode ajudar?
-
Micael
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Jan 31, 2013 00:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Qui Abr 18, 2013 11:47
por nakagumahissao » Qui Abr 18, 2013 11:47
Veja bem, temos dois triângulos semelhantes:
TQO e TQP. A distância entre OQ será de 6 -x e QP de 16 - 6 + x = 10 + x. Logo:

Note que OQ = 6-x, QP = 16 - (6-x) = 10 + x, PTO é um triângulo retângulo pois PT é tangente ao círculo, TQO e TQP são triângulos retângulos. Logo, de PTO tem-se:
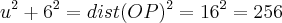
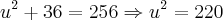
Agora, do triângulo OQT tem-se:
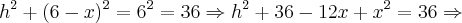
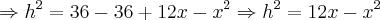
Do último triângulo, TQP, tem-se:
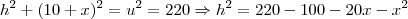
Igualando
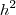
:
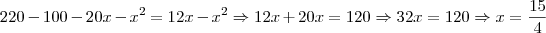
Sabendo-se que x = 15/4 e que OP = 16, então a distância QP = 10 + x será de:
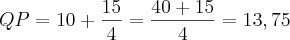
Que é o valor procurado!
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Micael » Seg Abr 22, 2013 19:15
por Micael » Seg Abr 22, 2013 19:15
Muito obrigado pela ajuda... valeu mesmo
-
Micael
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Jan 31, 2013 00:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8725 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4718 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4826 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2541 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
-
- geometria plana
 por Abner » Seg Jan 31, 2011 17:53
por Abner » Seg Jan 31, 2011 17:53
- 3 Respostas
- 3681 Exibições
- Última mensagem por Abner

Ter Fev 01, 2011 17:31
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






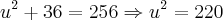
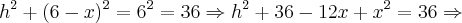
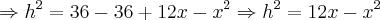
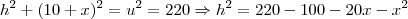
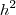 :
: