Para se construir um pássaro através dessatécnica, usou-se uma folha de papel,quadrada, com 2dm de lado, representadana figura 1.
O primeiro passo foi dobrar opapel, fazendo os lados DA e DC doquadrado coincidirem com o segmento DG sobre a diagonal DB desse quadrado,obtendo-se um quadrilátero DEBF, representado na figura 2.


A área doquadrílatero DEBF,em dm², mede:
A)
![4\sqrt[2]{2} - 4 4\sqrt[2]{2} - 4](/latexrender/pictures/fd5bb1ec5df0932dee2276a5e9fa6d05.png)
B)
![8 - 4\sqrt[2]{2} 8 - 4\sqrt[2]{2}](/latexrender/pictures/93a62d53a9b488f6fcd9ef45688516c6.png)
C)
![2\sqrt[2]{2} 2\sqrt[2]{2}](/latexrender/pictures/ee13a83dd86f943ecf5c04d9e0e519d2.png)
D)
![1 + \sqrt[2]{2} 1 + \sqrt[2]{2}](/latexrender/pictures/646d9a4a75980f4b264d416b9a9e2d95.png)
E)
![2 + 4\sqrt[2]{2} 2 + 4\sqrt[2]{2}](/latexrender/pictures/9bf304f0835697be49658e562d897714.png)
Eu estou com dúvidas nessa questão..a inicio de conversa, considere a reta EF a base do triângulo hachurado.
Eu sei que, de D a G mede 2dm, chamei a medida de DF e DE de
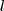 e a medida de BF e BE de
e a medida de BF e BE de  ..eu sei que os triangulos [Unparseable or potentially dangerous latex formula. Error 2 ] (área) e creio eu que a reta DG é
..eu sei que os triangulos [Unparseable or potentially dangerous latex formula. Error 2 ] (área) e creio eu que a reta DG é 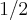 do diâmetro, e a reta GB é
do diâmetro, e a reta GB é 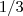 ..
..Eu tentei usar realão de quadrilátero *losângulo, mas não consegui achar a medida de EF..se fosse um triângulo equilátero ficava fácil, mas creio eu que não se trata de um triangulo equilátero, ai me compliquei mais ainda. e até agora não achei um jeito de responder essa questão.
Se poderem me dar uma LUZ com ela, agradeço muito.
OBS: DESCULPEM-ME PELO MEU QUADRADO E TRIÂNGULO MAL FEITO


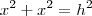
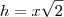
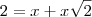

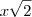
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.