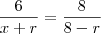por Gustavo Gomes » Sáb Out 06, 2012 22:07
por Gustavo Gomes » Sáb Out 06, 2012 22:07
Olá.
Estou com dificuldade em resolver um problema do volume 9 (Geometria Plana) da coleção 'Fundamentos da Matemática Elementar' DOLCE, O. POMPEU, J.N., para a determinação do raio do círculo, sendo que o triângulo retângulo possui catetos de medidas 6 e 8.
Tentei utilizar semelhança (de triângulos), mas não consegui associação entre lados de triângulo e diâmetro do círculo, neste caso.
Abraços.
- imagem
Editado pela última vez por
Gustavo Gomes em Sáb Out 06, 2012 22:33, em um total de 3 vezes.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por young_jedi » Sáb Out 06, 2012 22:14
por young_jedi » Sáb Out 06, 2012 22:14
Amigo não tem com voce colocar a figura?
Ajudaria bastante
Pra colocar aqui no forum sugiro que voce salve ele com .jpg
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Gustavo Gomes » Sáb Out 06, 2012 22:19
por Gustavo Gomes » Sáb Out 06, 2012 22:19
Pois é, young jedi, estou tentando postar a figura mas não estou conseguindo...., mesmo em .jpg.... vou tentando aqui... Se puder me ajudar, agradeço.
Abraços.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por young_jedi » Sáb Out 06, 2012 22:21
por young_jedi » Sáb Out 06, 2012 22:21
voce tem que ir em adicionar anexo nas opções a abaxio da caixa que voce escreve a mensagem e depois ir em adicionar na mensagem, voce esta fazendo isto?
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Gustavo Gomes » Sáb Out 06, 2012 22:34
por Gustavo Gomes » Sáb Out 06, 2012 22:34
Agora consegui!! Valeu pela dica.
Obrigado.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por young_jedi » Sáb Out 06, 2012 22:44
por young_jedi » Sáb Out 06, 2012 22:44
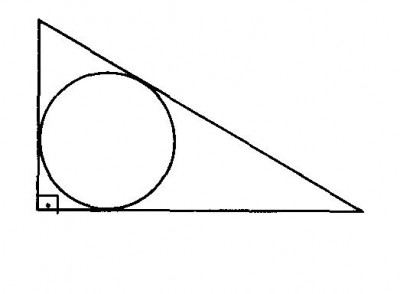
- triangulo
- imagem.JPG (17.42 KiB) Exibido 4593 vezes
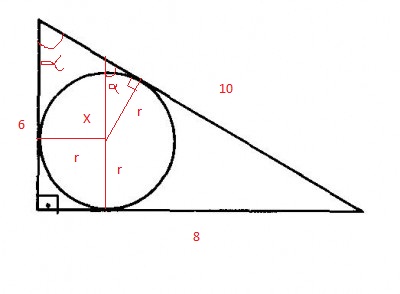
por semelhança de triangulos
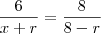

fazendo semelhança com o triangulo menor

substituindo o x da relação anterior voce encontra uma equação de r e resolvendo acha o valor de r
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Gustavo Gomes » Sáb Out 06, 2012 22:59
por Gustavo Gomes » Sáb Out 06, 2012 22:59
Obrigado, young jedi!!!
Ótimo raciocínio.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por jeanderson09 » Qua Out 10, 2012 20:57
por jeanderson09 » Qua Out 10, 2012 20:57
cara o negocio e o seguinte.....
ha uma formula que diz que o raio de um circulo inscrito em um triangulo retangulo é igual ao semiperimetro menos a hipotenusa....
se os catetos sao 6 e 8.....a hipotenusa ira ser 10
ai voce faz o semiperimetro que vai dar 12 e tira 10 que vai dar 2
raio do circulo vai ser igual a 2
Editado pela última vez por
jeanderson09 em Qui Out 11, 2012 21:07, em um total de 1 vez.
-
jeanderson09
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Out 10, 2012 20:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Gustavo Gomes » Qua Out 10, 2012 23:25
por Gustavo Gomes » Qua Out 10, 2012 23:25
Verdade, jeanderson09!!!!! Valeu, obrigado.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por jeanderson09 » Qui Out 11, 2012 21:09
por jeanderson09 » Qui Out 11, 2012 21:09
de nada....fico feliz por ter ajudado

-
jeanderson09
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Out 10, 2012 20:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercícios de triangulos retangulos
por analuiza » Qua Fev 16, 2011 16:52
- 1 Respostas
- 5816 Exibições
- Última mensagem por DanielRJ

Qua Fev 16, 2011 20:13
Trigonometria
-
- [Áreas: Triângulos retângulos] Razão áurea
 por Gustavo Gomes » Sex Out 19, 2012 22:58
por Gustavo Gomes » Sex Out 19, 2012 22:58
- 1 Respostas
- 1495 Exibições
- Última mensagem por e8group

Sáb Out 20, 2012 01:24
Geometria Plana
-
- [Circunscrição de sólidos] Esfera e octaedro regular
por adlehs » Qui Nov 12, 2015 03:01
- 2 Respostas
- 4530 Exibições
- Última mensagem por adauto martins

Sáb Nov 14, 2015 15:00
Geometria Espacial
-
- retângulos
 por nordau » Seg Jan 27, 2014 13:29
por nordau » Seg Jan 27, 2014 13:29
- 0 Respostas
- 1005 Exibições
- Última mensagem por nordau

Seg Jan 27, 2014 13:29
Geometria Plana
-
- Quantos retângulos?
por Fernanda Lauton » Qui Abr 08, 2010 18:04
- 0 Respostas
- 1239 Exibições
- Última mensagem por Fernanda Lauton

Qui Abr 08, 2010 18:04
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.