 por Jhenrique » Qua Jul 25, 2012 02:51
por Jhenrique » Qua Jul 25, 2012 02:51
meus caros, saudações!
Assisti um vídeo do IMPA (um vídeo maravilhoso!) sobre construções geométricas... o Wagner desenhava com régua e compasso qualquer fórmula!
Ele demonstrou, algebricamente e geometricamente, que a média geometrica [x] de dois valores [a, b] é igual a ?ab.
Entretanto, ele também afirmou que a terceira proporcional é igual a média geométrica, ou seja: a/x=x/b <=> x=?ab.
Consultando o google e o site somatematica, notei que a definição de 3ª proporcional não é a/x=x/b <=> x=?ab como o wagner definiu, e sim: a/b=b/x => x=b²/a.
Como assim, é possível ter quantas interpretações para o conceito de 3ª proporcional?
Quem está certo, quem está errado??
agradeço os esclarecimento,
José h
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por DanielFerreira » Dom Ago 05, 2012 16:20
por DanielFerreira » Dom Ago 05, 2012 16:20
Jhenrique,
segundo a definição,
Uma proporção onde os meios são iguais, um dos extremos é a terceira proporcional do outro extremo, temos:
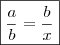
Analisando a afirmação feita pelo Wagner (com base no que vc disse) pude concluir que é verdadeira, mas, quando

, veja:
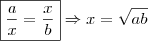
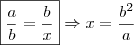
Igualando-as:
![\sqrt[]{ab} = \frac{b^2}{a} \\\\\\ \left( \sqrt[]{ab}\right)^2 = \left( \frac{b^2}{a}\right)^2 \\\\\\ ab = \frac{b^4}{a^2} \\\\ a^3b = b^4 \\\\ a^3 = b^3 \\\\ \boxed{\boxed{a = b}} \sqrt[]{ab} = \frac{b^2}{a} \\\\\\ \left( \sqrt[]{ab}\right)^2 = \left( \frac{b^2}{a}\right)^2 \\\\\\ ab = \frac{b^4}{a^2} \\\\ a^3b = b^4 \\\\ a^3 = b^3 \\\\ \boxed{\boxed{a = b}}](/latexrender/pictures/f2e2510ac94135e65e4cbef2bcf0c2ee.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão Proporcional-Grandeza proporcional e inversamente
por AlexandreLuna » Ter Abr 24, 2012 22:10
- 2 Respostas
- 2662 Exibições
- Última mensagem por jrmatematico

Dom Mai 13, 2012 10:02
Matemática Financeira
-
- Divisão proporcional
por karenblond » Seg Ago 29, 2011 23:23
- 3 Respostas
- 2698 Exibições
- Última mensagem por Neperiano

Qua Ago 31, 2011 14:58
Sistemas de Equações
-
- DIVISÃO PROPORCIONAL
por Ailton » Ter Fev 21, 2012 01:47
- 0 Respostas
- 1482 Exibições
- Última mensagem por Ailton

Ter Fev 21, 2012 01:47
Matemática Financeira
-
- Divisão Proporcional
por Raphael Feitas10 » Ter Nov 27, 2012 00:25
- 0 Respostas
- 1622 Exibições
- Última mensagem por Raphael Feitas10

Ter Nov 27, 2012 00:25
Equações
-
- diretamente proporcional
por dandara » Sex Abr 22, 2016 12:49
- 2 Respostas
- 2227 Exibições
- Última mensagem por dandara

Dom Abr 24, 2016 10:14
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


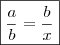
 , veja:
, veja: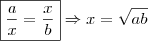
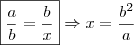
![\sqrt[]{ab} = \frac{b^2}{a} \\\\\\ \left( \sqrt[]{ab}\right)^2 = \left( \frac{b^2}{a}\right)^2 \\\\\\ ab = \frac{b^4}{a^2} \\\\ a^3b = b^4 \\\\ a^3 = b^3 \\\\ \boxed{\boxed{a = b}} \sqrt[]{ab} = \frac{b^2}{a} \\\\\\ \left( \sqrt[]{ab}\right)^2 = \left( \frac{b^2}{a}\right)^2 \\\\\\ ab = \frac{b^4}{a^2} \\\\ a^3b = b^4 \\\\ a^3 = b^3 \\\\ \boxed{\boxed{a = b}}](/latexrender/pictures/f2e2510ac94135e65e4cbef2bcf0c2ee.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
