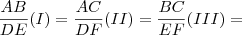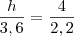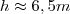por marioluis » Seg Jul 09, 2012 19:58
por marioluis » Seg Jul 09, 2012 19:58
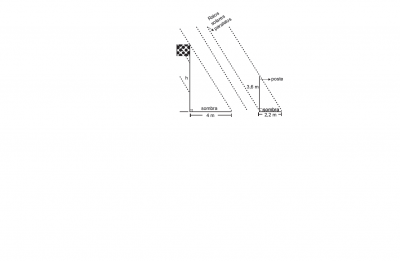
- Imagem do problema
Minha dúvida se refere a uma questão sobre um triângulo retângulo e sua altura nessa questão é dado alguns dados mas eles ficam confusos, até consegui achar o valor aproximado mas não de uma forma que se alinhe com um raciocinio lógico.Peço se alguem poder me ajudar na resolução desse problema ficarei agradecido.
Em um certo instante do dia, o sol projetou a sombra de um mastro de São João sobre o pátio de uma fazenda.No mesmo instante, um poste de luz situado na mesma horizontal desse mastro, teve também sua sombra projetada.A medida da altura desse mastro é aproximadamente de ?
-
marioluis
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jul 07, 2012 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Seg Jul 09, 2012 20:20
por Arkanus Darondra » Seg Jul 09, 2012 20:20
marioluis escreveu:Minha dúvida se refere a uma questão sobre um triângulo retângulo e sua altura nessa questão é dado alguns dados mas eles ficam confusos, até consegui achar o valor aproximado mas não de uma forma que se alinhe com um raciocinio lógico.
Poste o que você fez. Possivelmente está correto, visto que o exercício pede um valor aproximado.
marioluis escreveu:Peço se alguem poder me ajudar na resolução desse problema ficarei agradecido.
Como os raios incidentes são paralelos entre si, os triângulos possuem ângulos internos de mesmo valor.
Portanto, os triângulos são
semelhantes pelo caso AA e seus
lados correspondentes possuem uma
razão de semelhança constante (k).
Tente concluir.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por marioluis » Seg Jul 09, 2012 21:53
por marioluis » Seg Jul 09, 2012 21:53
Arkanus Darondra escreveu:marioluis escreveu:Minha dúvida se refere a uma questão sobre um triângulo retângulo e sua altura nessa questão é dado alguns dados mas eles ficam confusos, até consegui achar o valor aproximado mas não de uma forma que se alinhe com um raciocinio lógico.
Poste o que você fez. Possivelmente está correto, visto que o exercício pede um valor aproximado.
marioluis escreveu:Peço se alguem poder me ajudar na resolução desse problema ficarei agradecido.
Como os raios incidentes são paralelos entre si, os triângulos possuem ângulos internos de mesmo valor.
Portanto, os triângulos são
semelhantes pelo caso AA e seus
lados correspondentes possuem uma
razão de semelhança constante (k).
Tente concluir!
Veja bem o que eu fiz:
como os angulos são iguais e a incidencia dos raios são as mesmas eu simplimente subitrai 2,2 m de 3,6 m,e adicionei ao valor 1,2m a sombra do Poste dando aproximadamente 5,4 m.
-
marioluis
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jul 07, 2012 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Seg Jul 09, 2012 22:25
por Arkanus Darondra » Seg Jul 09, 2012 22:25
marioluis escreveu:como os angulos são iguais e a incidencia dos raios são as mesmas eu simplimente subitrai 2,2 m de 3,6 m,e adicionei ao valor 1,2m a sombra do Poste dando aproximadamente 5,4 m.
O fato de os ângulos internos dos triângulos e a incidência dos raios serem iguais não justifica o que foi feito.

Como os triângulos ABC e DEF são semelhantes, vem:
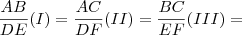 k
kDe I e III, vem:
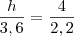
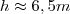

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por marioluis » Ter Jul 10, 2012 08:53
por marioluis » Ter Jul 10, 2012 08:53
Arkanus Darondra escreveu:marioluis escreveu:como os angulos são iguais e a incidencia dos raios são as mesmas eu simplimente subitrai 2,2 m de 3,6 m,e adicionei ao valor 1,2m a sombra do Poste dando aproximadamente 5,4 m.
O fato de os ângulos internos dos triângulos e a incidência dos raios serem iguais não justifica o que foi feito.

Como os triângulos ABC e DEF são semelhantes, vem:
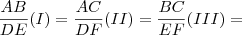 k
kDe I e III, vem:
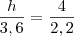
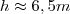

Muito obrigado,pela sua ajuda e atenção!!
-
marioluis
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jul 07, 2012 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo de x em função de a, Geometria Plana]
por Lenin » Qui Abr 11, 2013 00:16
- 2 Respostas
- 2922 Exibições
- Última mensagem por Lenin

Qui Abr 11, 2013 20:03
Geometria Plana
-
- [GEOMETRIA PLANA] Cálculo de área
 por eulalia » Seg Abr 20, 2015 16:40
por eulalia » Seg Abr 20, 2015 16:40
- 0 Respostas
- 2374 Exibições
- Última mensagem por eulalia

Seg Abr 20, 2015 16:40
Geometria Plana
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8725 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4713 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4825 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.